Palestrantes Confirmados:
| Sexta (22/11) | Sábado (23/11) | Domingo (24/11) | |
| Manhã | As atividades do turno da manhã ocorrerão no Teatro Universitário 8h – 9h Credenciamento 8h30min Atividade Cultural: Apresentação da Banda de Congo Capixaba “Panela de Barro”. 9h – 10h Cerimônia de Abertura e Atividade Cultural 10h – 11:30 Mesa Redonda I “Novo PROFMAT e perspectivas para a formação do professor” | 8h – 9h Comunicações Orais 9h – 10:30 Mesa Redonda III “Discussões e reflexões sobre BNCC na Educação Básica” Parte II 10h30min – 12h30min Grupos de Trabalhos – Edição Especial “Jornada BNCC para o Ensino Fundamental I e II” | 8h – 9h Comunicações Orais 9h – 10h Palestra I “Contribuições do Lesson Study para o ensino e aprendizagem de Matemática” 10h – 11h30min Plenária dos Grupos de Trabalhos 11h30min – 12h30min Palestra II “Fronteiras entre as disciplinas não existiam” |
| Tarde | 13h – 15h Minicurso I – Parte I 15h – 16h30min Apresentação de pôsteres e Café com a ANPMat: Exposição “Mulheres na Matemática” Exposição “Gabinete da Matemática” Exposição “Mostra de Matemática DMAT/UFES” 16h30min – 18h – Minicurso I – Parte II 18h – 19h30min Mesa Redonda II “Discussões e reflexões sobre a BNCC na Educação Básica” Parte I | 13h30min – 15h30min Minicurso II – Parte I 15h30min – 17h Apresentação de pôsteres e Café com a ANPMat: Exposição “Mulheres na Matemática” Exposição “Gabinete da Matemática” Exposição “Mostra de Matemática DMAT/UFES” 17h – 18h30min Minicurso II – Parte II |
A cerimônia de abertura será transmitida ao vivo pelo link https://video.rnp.br/portal/transmissao/simposio-nacional-4
Mesa Redonda I – “Novo PROFMAT e perspectivas para a formação do professor”.
Convidados: Hilário Alencar (UFAL), Marcelo Viana (IMPA) e Vanderlei Horita (UNESP).
Mediador: Antônio Cardoso do Amaral – Escola Augustinho Brandão – Cocal dos Alves/PI
Mesa Redonda II – “Discussões e reflexões sobre a BNCC na Educação Básica” Parte I
Convidados: Cydara Ripoll (UFRGS), Letícia Rangel (Cap UFRJ), Sérgio Lopes (UNICERP).
Mediadora: Letícia Rangel
Mesa Redonda III – “Discussões e reflexões sobre a BNCC na Educação Básica” Parte II
Convidados: Carmen Mathias (UFSM), Flávia Landim (UFRJ), Humberto Bortolossi (UFF).
Mediador: Sérgio Lopes
Grupos de Trabalhos – Edição Especial – “Jornada BNCC para o Ensino Fundamental I e II”
GT1 – Números. Coordenadoras: Letícia Rangel (Cap UFRJ) e Renata Magarinus (IFRS)
GT2 – Álgebra. Coordenadores: Sérgio Lopes (UNICERP) e Marcela Luciano Vilela de Souza (UFTM)
GT3 – Geometria, Grandezas e Medidas. Coordenadoras: Carmen Mathias (UFSM) e Ana Luiza Kessler (CAP – UFRGS)
GT4 – Probabilidade e Estatística. Coordenadores: Flávia Landim (UFRJ) e Vitor Amorim (IFSP – SP)
Palestra I – “Contribuições do Lesson Study para o ensino e aprendizagem de Matemática”
Palestrante: Julia Wrobel (UFES)
Resumo: O Lesson Study tem origem japonesa e pode ser traduzido como estudo/pesquisa da prática do professor. Destaca a importância do trabalho docente colaborativo por meio de investigação, estudo e reflexão sobre a matemática escolar e as práticas em sala de aula. Apresentaremos aulas desenvolvidas com aspectos do Lesson Study em escolas capixabas de educação básica e na Licencatura em Matemática na UFES.
Palestra II – “Fronteiras entre as disciplinas não existiam”
Palestrante: Flávia Landim (UFRJ)
Resumo: Pretende-se apresentar um breve histórico do desenvolvimento da Estatística, destacando seu caráter essencialmente interdisciplinar. Em seguida, o conteúdo de Estatística e Probabilidade na Educação Básica a partir de recomendações de pesquisadores em Educação Estatística e em acordo com a BNCC será considerado. Propostas de abordagem integrada de Estatística e Probabilidade na Educação Básica serão discutidas a partir de atividades retiradas de livros didáticos.
Atividade Cultural: Apresentação da Banda de Congo Capixaba “Panela de Barro”.
“A Banda de Congo Panela de Barro do bairro Goiabeiras, Vitória ES, foi fundada em 1938.
As cantadeiras e os congueiros sob o comando dos mestres Valdemiro Sales e Vinícius Loreto cantam, tocam e dançam em reverência ao Santo de devoção São Benedito. A Festa de São Benedito da Banda de Congo Panela de Barro acontecerá no dia 25 de dezembro de 2019. “
Exposição: “Gabinete da Matemática”
O Gabinete da Matemática é uma ação do grupo PIBID da Matemática da Universidade Federal Fluminense em Niterói que tem como principal objetivo a divulgação matemática. Por meio de seus vários artefatos, esse pequeno museu, orientado para o público escolar, tem por objetivo despertar a curiosidade, estimular a apreciação e o gosto da matemática e suas conexões. Para maiores informações acesse http://im-uff.mat.br/gabinete/
Exposição: “Mulheres na Matemática”

Exposição de posters sobre mulheres matemáticas, organizada por Adriana Neumann (UFRGS) e Cydara Cavedon Ripoll(UFRGS) para o II Festival da Matemática do RS.
É composta por 5 temáticas:
1. Matemáticas do passado: Resgate da história de algumas matemáticas ilustres tais como Hipátia de Alexandria e outras.
Fonte o livro “História de Hipátia e de muitas outras matemáticas” de Cecília Fernandez, Ana Maria Luz e Isabela Viana.
2. Depoimentos de Matemáticas de vários países retirados do documentário criado pelo IMU Committee for Women in Mathematics, disponível em https://www.youtube.com/watch?v=uNJ7riiPHOY
3. “Maryam Mirzakhani Remember exhibition”
Maryam Mirzakhani é a única mulher a ganhar a medalha Fields até o momento.
Curadora: Thaís Jordão. 0s direitos autorais pertencem ao CWM da IMU.

4. Levantamento da participação feminina (docentes e discentes) nas universidades federais do estado do RS.
5. Dados da OBMEP do ano de 2017 e as medalhistas de ouro gaúchas na OBMEP de 2018.
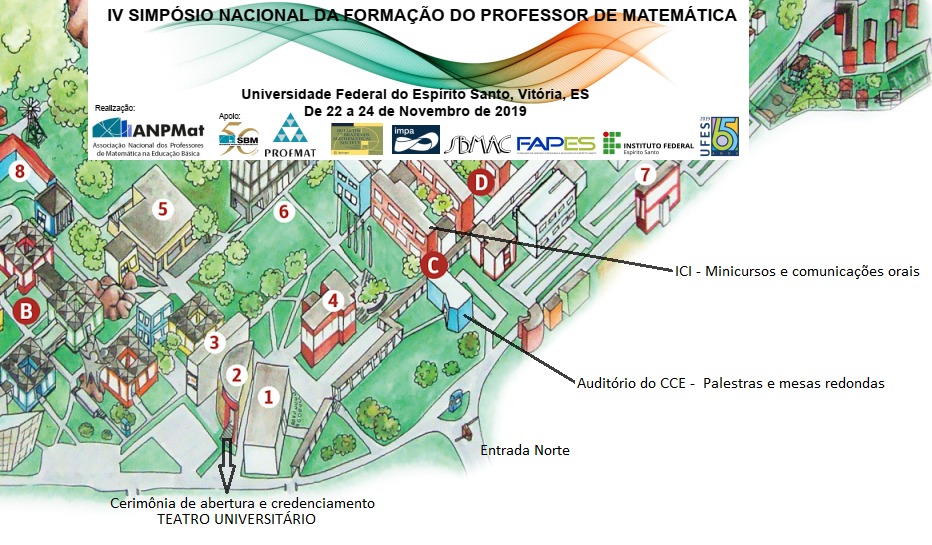
A cerimônia de abertura e o credenciamento (sexta-feira) ocorrerão no Teatro Universitário.
Os minicursos e comunicações orais ocorrerão no ICI.
Palestras e mesas redondas ocorrerão no Auditório do CCE (Centro de Ensino).
Para a inscrição nos minicursos e grupos de trabalho:
1) Acesse o link: http://eventos.anpmat.org.br
2) Clique em “Entrar”
3) Entre com seu login e senha
4) Clique em “Meus Eventos”
5) Clique em IV Simpósio Nacional da Formação do Professor de Matemática
6) Clique em “Atividades”
7) Marque as atividades que deseja
8) Clica em ” Inscrever-se”
Resumos Minicursos
1 – CARTÕES MÁGICOS E JOGOS DE SUBTRAÇÃO (Sexta-Feira)
Rogério Ricardo Steffenon
Neste minicurso serão apresentados dois tipos de cartões mágicos (binários e Fibonacci), jogos de subtração e alguns outros problemas interessantes. Muitos dos problemas abordados surgem em Olimpíadas de Matemática e podem ser uma boa fonte para professores estimularem seus alunos a estudar Matemática. O texto que contém boa parte desses tópicos é o ebook disponível em https://bit.ly/2j5aW0l O roteiro será o seguinte: cartões mágicos binários, sistema binário, cartões mágicos de Fibonacci, Teorema de Zeckendorf, Jogos de subtração (BINIM, FINIM, ZENIM, NIM clássico e outros), Problema de Josephus e Hotel de Hilbert.
2 – REGRESSÃO LINEAR E O MÉTODO DOS MÍNIMOS QUADRADOS: UMA INTRODUÇÃO PARA PROFESSORES DO ENSINO BÁSICO À LUZ DA BNCC (Sábado)
Humberto Bortolossi e David da Costa Pinho
Para tentar entender o mundo que nos cerca, uma questão que surge naturalmente é investigar se determinados fenômenos estão associados ou não. Tipicamente, estes fenômenos são descritos por variáveis quantitativas e, então, investiga-se se estas variáveis estão relacionadas (correlação) e, se este for o caso, qual é o tipo de relação funcional entre elas (regressão). Esses tópicos de Estatística desempenham um papel fundamental em várias áreas aplicadas. Dada a sua importância, o tema foi incluído na última versão da BNCC para o Ensino Médio (habilidade EM13MAT510). Contudo, o tópico é novo em termos de formação de professores. Neste contexto, o presente minicurso visa promover uma formação continuada abordando os seguintes temas: (1) uma breve revisão histórica da regressão linear; (2) uma demonstração simples, acessível para alunos do Ensino Médio, usando apenas funções quadráticas, para a fórmula de regressão linear dada pelo método dos mínimos quadrados; (3) indicações de como usar recursos tecnológicos (GeoGebra, LibreOffice e Excel) e (4) aplicações de regressão linear.
4 – JOGOS POPULARES PARA DESENVOLVER DESENVOLVENDO ALGUNS CONCEITOS MATEMÁTICOS (Sábado)
Helder de Carvalho Matos, Raimundo Bastos e Rui Seimetz
Nesse minicurso/oficina temos por objetivo vivenciar com os participantes a importância dos jogos para o ensino e a aprendizagem de alguns conceitos matemáticos. Por meio do uso de jogos os participantes aprendem a partir dos seus próprios erros, o que incentiva o mesmo, a pensar nas consequências de suas atitudes, facilitando a construção de seus próprios conceitos e da apropriação de conhecimento, incentiva desenvolvimento de organização, concentração, atenção, raciocínio lógico e o senso cooperativo entre os jogadores. Alguns dos conceitos matemáticos que serão desenvolvidos e usados são: Métodos de contagem; Congruência módulo n; Números escritos na base 2; Fórmula de Euler generalizada; Raciocínio Lógico.
5 – INTRODUÇÃO A GEOMETRIAS NÃO EUCLIDIANAS NOS ENSINOS FUNDAMENTAL II E MÉDIO: UMA ABORDAGEM SIGNIFICATIVA, CONTEXTUALIZADA E INTERDISCIPLINAR (Sexta-feira)
Marlon Mülhbauer, Lucas dos Santos Maciel
Este minicurso tem objetivo principal de propor a introdução do conteúdo de geometrias não Euclidianas nos ensinos fundamental II e médio. Serão retomados alguns tópicos de História da Matemática, conceitos de álgebra vetorial e trigonometria. Também serão propostas atividades com material concreto para melhor compreensão dos conceitos, identificando semelhanças e diferenças entre a geometria Euclidiana e as geometrias não Euclidianas. A interdisciplinaridade com a disciplina de geografia estará presente, quando se associam as definições e propriedades de geometria Esférica com Cartografia. Além disso, será desenvolvida com os participantes uma sequência didática para aplicar com seus alunos, com lista de exercícios, atividades práticas, uso da calculadora científica e planilhas para aprofundar o aprendizado, obtendo dois resultados importantes: a determinação da menor distância entre dois pontos de uma esfera e uma propriedade relativa à soma dos ângulos internos de um triângulo esférico.
6 – DESAFIOS E POSSIBILIDADES NO ENSINO DE MATEMÁTICA PARA ALUNOS COM DEFICIÊNCIA VISUAL (Sábado)
Fábio Bernardo e Cláudio Dias
O minicurso tem por objetivo apresentar e discutir as concepções sobre o uso de recursos e materiais didáticos acessíveis para o ensino de matemática para alunos com DV, estendendo e ampliando essas concepções para além dos objetos materiais, incluindo ainda a utilização de softwares que que podem favorecer e minimizar as dificuldades desses alunos no aprendizado de matemática. O trabalho tem sido realizado em duas escolas públicas federais na cidade do RJ, a primeira especializada na educação de pessoas com DV e a segunda, uma escola inclusiva que recebe e atende alunos com DV há muitos anos. O minicurso se propõe a familiarizar os cursistas com a leitura e escrita matemática em braille, a utilização problematizada do geoplano e do multiplano, a produção artesanal de materiais grafo-táteis e a utilização do software livre Monet como um recurso para a confecção e adaptação de gráficos matemáticos acessíveis para alunos com DV. Este trabalho é resultado de estudos e pesquisas desenvolvidos pelos autores, tem como público alvo os professores da Educação Básica e alunos dos cursos de Licenciatura em matemática e os recursos e metodologias a serem discutidas e desenvolvidas no minicurso fazem parte da rotina de trabalho dos autores.
7 – MODELOS DE EXPLORAÇÃO MATEMÁTICA NA PLATAFORMA DESMOS: ENSINAR E APRENDER EM UM AMBIENTE VIRTUAL DE APRENDIZAGEM (Sábado)
Gladson Antunes, Michel Cambrainha
O Desmos (www.desmos.com) é uma plataforma online de exploração matemática (ambiente virtual de aprendizagem) que surpreende à medida que oferece inúmeras possibilidades para a sala de aula. Neste minicurso exploraremos algumas atividades da plataforma Desmos focando nas ferramentas disponíveis para o professor e em como elas podem contribuir para a inovação na sala de aula que usa tecnologias. Além disso, a maneira de concepção dessas atividades convida o professor a pensar suas aulas de maneira diferente, proporcionando uma espécie de transformação digital na maneira de conceber e executar sua didática. Durante o minicurso as atividades serão executadas por todos os participantes em computadores ou em seus smartphones.
8 – UNIDADES DE MEDIDA E ORDEM DE GRANDEZA: “ATIVIDADES DO LIVRO ABERTO DE MATEMÁTICA” (Sábado)
Bruno Vianna Santos, Maria de Fátima P. Almeida e Luiz Amorim Duarte
Neste minicurso os participantes estarão diante de uma proposta inovadora sobre o tema unidades de medidas. Com atividades que tem um caráter de experimentação, temas que envolvem a necessidade de medir, de padronizar, de expressar medidas; as medidas usadas na informática, as medidas compostas por outras, notação científica, ordem de grandeza e precisão, aparecem num ambiente por vezes laboratorial, por vezes imersivo, que permite a cada participante um mergulho nas condições que compõem esses saberes. Esse minicurso se baseia em atividades do capítulo: “Unidades de Medida e Ordem de Grandeza” do Projeto “Livro Aberto de Matemática”, que é uma realização do IMPA e da OBMEP, com apoio financeiro do Itaú Social, que tem como objetivo principal a produção de livros didáticos de matemática com licença aberta a partir de um trabalho colaborativo.
9 – SOFTWARE TRACKER: MATEMÁTICA E FÍSICA (Sábado)
Weber H. M Feu, Fabrício A.Castro e João Batista Q. Zuliani
Apresentaremos nesta oficina o software Tracker e o relato da experiência de atividades de integração entre as disciplinas matemática e física que foram desenvolvidas com estudantes de primeiro ano de ensino médio. Em tais atividades, que serão realizadas também pelos participantes, será realizada a análise de cenas com o software Tracker, a sua modelagem matemática e uso do Geogebra para simular a cena em estudo e representar os resultados. Espera-se que este minicurso motive os professores a desenvolverem suas próprias atividades integrando os conteúdos de matemática e física. Observamos que o desenvolvimento das tarefas pelos estudantes proporcionou a elaboração de conjecturas e a discussão das ideias.
10 – OFICINA DE JOGOS DIDÁTICOS DO GEMAT-UERJ (Sexta-feira)
Leandro Machado, Pedro Teba, Guilherme Silva , Manuela Correia, Gabriel Cacau e Thiago Cunha
O objetivo desta oficina é apresentar possibilidades de utilização de Jogos nas aulas de Matemática da Educação Básica, não apenas como disparador dos conceitos, mas também como recursos para aprofundamento. Na primeira parte, os participantes passarão por seis estações que trabalham conteúdos diversos dos Ensinos Fundamental e Médio. Em cada estação, há um jogo a ser disputado e um roteiro de ação, com questões que surgem a partir da própria atividade, abrindo discussões sobre a transição do lúdico para o teórico. Posteriormente, apresentaremos uma série de jogos que visam desenvolver dois conteúdos específicos: Números Relativos e Equações do 2º Grau, promovendo um debate sobre a construção de Sequências Didáticas baseadas na Ludicidade.
11 – JOGOS MATEMÁTICOS COM LÁPIS E PAPEL (Sexta-feira)
Elisa Fonseca Sena e Silva, Ana Cristina Pinheiro Fernandes Meira, Sarah Rafaely Santos, Tayná Elias Santos e José Monteiro Hilário da Silva
A utilização de jogos em sala de aula é importante para que os estudantes modifiquem a forma com que encaram os erros. No entanto, muitas vezes os professores, sobrecarregados de atividades, não os utilizam por falta de tempo para confeccioná-los. É nesse sentido que esta oficina foi elaborada: pretendemos apresentar jogos matemáticos de fácil reprodução, que utilizem somente uma folha de papel impressa e que sejam versáteis o suficiente para serem modificados para abordarem outros conteúdos. Com o jogo “Calc Plus” é possível abordar não só as quatro operações básicas, mas várias outras. O “Bingo das funções” pode trabalhar um tipo de função específica ou pode ser adaptado para outros conteúdos. O jogo “Quem sou eu geométrico” trata de triângulos e quadriláteros, mas pode ser modificado de acordo com o interesse do professor. Já a conhecida “Batalha Naval” trabalha o plano cartesiano.
12 – O MATH ESCAPE ROOM COMO UM RECURSO DIDÁTICO PARA O ENSINO DA MATEMÁTICA (Sexta-feira)
Juliana Campos Sabino de Souza, Paulo Borges, Brenner Alvim, Stephanie Machado da Silva e Matheus Procópio de Quadros
O uso de tecnologias para o aprendizado vêm se tornando cada vez mais comuns nos dias de hoje. Pensando nas dificuldades perceptivas dos estudantes de matemática desde a educação básica até o ensino superior, desenvolvemos um aplicativo que utiliza realidade aumentada para auxiliar o processo de ensino-aprendizado de alunos com relação aos conceitos da geometria plana e espacial. Trazendo para sala de aula uma metodologia dinâmica e com a capacidade de criação de figuras em geometria plana e com a reprodução de poliedros em três dimensões, além de contar com conteúdo próprio e animado e reproduzido em realidade aumentada. A oficina terá atividades de construção de figuras, a apresentação de como lidar com alguns conceitos tanto da geometria plana quanto da espacial e a realização de exercícios com o auxílio do aplicativo proporcionando uma perspectiva em três dimensões das figuras apresentadas nos problemas.
13 – CRITÉRIOS DE DIVISIBILIDADE NA ESCOLA: UM TRABALHO DE REFLEXÃO DE GRUPO (Sexta-feira)
Luisa Rodríguez Doering e Cydara Cavedon Ripoll
Resumo: Este minicurso propõe uma reflexão de grupo aos professores da Escola Básica, incluindo Anos Iniciais, sobre critérios de divisibilidade. Parte de uma discussão sobre as ideias envolvidas nos critérios de divisibilidade que estão recomendados na Base Nacional Comum Curricular para o 6º ano, elaborando-se, com os participantes, argumentos que culminem em diferentes demonstrações. A seguir, desafia os participantes a adequarem tais demonstrações aos diferentes segmentos do Ensino Básico (anos iniciais, segundo segmento do Ensino Fundamental e Ensino Médio), contemplando, assim, as ideias de Hanna (1995) de defender que demonstrações voltem às salas de aula, principalmente aquelas “que explicam”. Desta forma, objetiva-se promover: o pensamento matemático na Escola Básica, especificamente, raciocínio e prova Stylianides (2009); uma maior ligação entre a ciência matemática e a prática da sala de aula (Klein, 2009); a formação continuada de professores e um aprimoramento do seu conhecimento de matemática para o ensino.
14 – UMA INTRODUÇÃO À COMPUTAÇÃO ALGÉBRICA: RESOLVENDO ALGEBRICAMENTE UM SHIDOKU (Sábado)
Cid de Araujo Moraes e Patrícia Erthal de Moraes
Neste minicurso apresentamos uma introdução à teoria das Bases de Gröbner com o objetivo de resolver sistemas de equações polinomiais. Essas Bases generalizam o processo de eliminação Gaussiana para polinômios de várias indeterminadas. Mostraremos como os cálculos das Bases de Gröbner podem ser usados para resolver algebricamente um quebra-cabeça Shidoku (uma versão reduzida do conhecido Sudoku). Estudaremos alguns pré-requisitos necessários da Álgebra como o Algoritmo da Divisão e da Pseudodivisão até a Teoria das Bases de Gröbner com os S-polinômios e o Algoritmo de Buchberger. Para dar suporte aos cálculos necessários, bem como, para a implementação da resolução algébrica do Shidoku, utilizaremos o sistema de computação algébrica CoCoA, que tem como aplicação principal o cálculo com polinômios em várias indeterminadas.
15 – MODELAGEM MATEMÁTICA EM 3 ATOS DE DAN MEYER: UMA METODOLOGIA DE ENSINO-APRENDIZAGEM NA ESCOLA BÁSICA APOIADA NA TEORIA DAS NARRATIVAS (STORYTELLING) (Sexta-feira)
Humberto José Bortolossi, Felipe Alexandre Inácio, Carolina Domingues Simões Martins, Ana Letícia da Silva de Mello, Carlos Vieira Reduzino Junior, João Pedro Teixeira de Sá, Thamilys Vasquez Elias Pereira e Thaiza Copello dos Santos
Em geral, os problemas de matemática têm um enunciado padrão: uma pequena história que apresenta os dados com uma pergunta no final. Com esse formato prototípico, o aluno não precisa entender o contexto do problema para resolvê-lo, pois basta varrer o texto do enunciado, identificar os dados e “jogá-los” na fórmula correta. Frente a essa situação, o educador Dan Meyer propõe uma metodologia diferente inspirada na estrutura narrativa de 3 atos de filmes como Star Wars. O foco dessa metodologia está em (1) atrair a atenção do estudante logo de início com uma imagem ou vídeo instigantes, (2) colocá-lo como ator do problema no sentido de determinar quais são as perguntas relevantes e quais são os dados necessários para resolver o problema e (3) o momento de resolução da expectativa com a apresentação da solução do problema, também em forma de uma imagem ou vídeo. Nesse contexto, essa oficina tem por objetivo apresentar a Modelagem Matemática em 3 Atos à comunidade de professores de Matemática, levando-os a vivenciar a metodologia de forma participativa e ativa.
16 – FUNÇÃO AFIM NO ENSINO MÉDIO: UMA PROPOSTA PARA O LIVRO ABERTO DE MATEMÁTICA (Sexta-feira)
Gladson Antunes e Michel Cambrainha
A pesquisa tem documentado diversas dificuldades dos estudantes com o conceito de função, também tem confirmado a ideia que muitos têm de que toda relação entre duas variáveis é proporcional. Muitos professores percebem em suas práticas a dificuldade que os estudantes têm para entender o conceito de inclinação de uma reta, havendo quase sempre confusões associadas ao cálculo dessa inclinação e à interpretação de funções lineares e afins e seus gráficos. Diante desse cenário, neste minicurso vamos apresentar a proposta do capítulo de Função Afim do Livro Aberto que está fundamentada em uma abordagem diferenciada que explora essas e outras dificuldades comuns que se colocam quando se estuda esses conceitos. Esperamos, com este minicurso, compartilhar experiências vividas durante a concepção e produção do texto, bem como aprender a partir das trocas que se estabelecerão durante os encontros, buscando estreitar ainda mais o relacionamento entre a matemática produzida na Universidade com a que é produzida na Escola. O capítulo de Função Afim foi desenvolvido pelos professores que ministrarão o minicurso em colaboração com o professor Bruno Viana do Colégio Pedro II do Rio de Janeiro, no âmbito do Projeto “Livro Aberto de Matemática” (http://umlivroaberto.com), uma iniciativa da OBMEP e do IMPA.
17 – PROBABILIDADE ALÉM DA COMBINATÓRIA – TÓPICOS E PROBLEMAS REAIS COM FOCO NO RACIOCÍNIO PROBABILÍSTICO (Sexta-feira)
Vitor Amorim e Graziele Mozer
A prática tradicional do ensino de Probabilidade e sua abordagem em textos didáticos frequentemente têm como foco problemas probabilísticos cuja principal competência exigida do aluno é a aplicação de técnicas de contagem estudadas previamente em Análise Combinatória. Apesar de sua inegável importância, o ensino de Probabilidade focado em problemas combinatórios de Probabilidade desenvolve nos alunos a falsa ideia de dependência e até mesmo de indissociabilidade entre Probabilidade e Análise Combinatória. O raciocínio probabilístico e o raciocínio combinatório são independentes e devem ser relacionados, quando adequado, e distinguidos, quando necessário. O foco excessivo em problemas combinatórios pode criar maiores dificuldades e uma desnecessária aversão do aluno à unidade temática de Probabilidade e Estatística, que ganhou destaque na BNCC. Por fim, tal prática acaba deixando em segundo plano aspectos fundamentais do raciocínio probabilístico, que têm consequências diretas em situações cotidianas e aplicações em diversos contextos da Ciência. Nesse cenário, este minicurso tem como objetivo dar destaque a algumas competências probabilísticas fundamentais, através da discussão da abordagem tradicional e, principalmente, da apresentação de tópicos e problemas de probabilidade do mundo real, cuja modelagem, em geral, não depende das técnicas de contagem, mas sim de uma compreensão significativa dos conceitos elementar es da Teoria das Probabilidades. Entre eles destacaremos a abordagem frequentista e a lei dos grandes números, a definição axiomática e as propriedades da probabilidade, probabilidade condicional e independência, probabilidade total, teorema de Bayes e a lei binomial. Ao final do minicurso, apresentaremos uma possibilidade de inovação no tratamento do tema no ensino médio, abordando três tópicos da área que não costumam ser trabalhados nesse segmento, mas que tem grande potencial de contextualização e integração com outras áreas da Matemática: a distribuição geométrica, as cadeias de Markov e a probabilidade geométrica.
18 – MATEMÁTICA NAS ESTAÇÕES DO ANO (Sábado)
Viviane de Oliveira Santos, Erenilda Severina da Conceição Albuquerque, Nickson Deyvis da Silva Correia, Franciely Lavine Silva de Lima e Wanessa Cavalcanti Oliveira
A oficina intitulada “Matemática nas estações do ano” é resultado da criação e aplicação de alguns materiais didáticos desenvolvidas no projeto de extensão “Sem mais nem menos” do Instituto de Matemática da Universidade Federal de Alagoas (Ufal). Os materiais propõem explorarmos a matemática presente nas estações do ano e nosso intuito com a oficina é motivar professores e futuros professores a construir tais materiais didáticos e até propor novas ideias de atividades relacionadas com o tema. Desta forma, iremos apresentar os materiais didáticos já desenvolvidos e aplicados em escolas e, posteriormente, os participantes construirão seus próprios materiais didáticos. No total são seis materiais didáticos, sendo quatro jogos e duas atividades. Esperamos que esta oficina possa trazer um ganho para os participantes no que diz respeito ao contato com outras possibilidades para o ensino e aprendizagem em matemática.
19 – MATEMÁTICA RECREATIVA: UMA PROPOSTA PARA SALA DE AULA (Sexta-feira)
Carmen Rosa Giraldo Vergara e Geovana Kelly Lino da Silva
Resumo: Neste minicurso serão realizadas atividades de Matemática Recreativa que podem ser usadas por professores dos Ensinos Fundamental e Médio para trabalhar diversos conceitos matemáticos. Inicialmente será apresentado o Museu da Matemática UFMG e a seguir serão explorados alguns quebra-cabeças geométricos e/ou atividades que fazem parte do acervo do Museu, dando orientações para sua aplicação em sala de aula. O minicurso será realizado de forma dinâmica e interativa, uma vez que parte do material concreto a ser utilizado será construído pelos participantes. Entre as atividades a serem trabalhadas se encontram, entre outros, o Teorema de Pitágoras (Disseção de Perigal), Dominós e Pentaminós, a geometria dos Caleidociclos e o jogo matemático HEX. Além disso, no final do minicurso, será promovida uma reflexão sobre dinâmicas que podem ser usadas para apresentar este material aos alunos em sala de aula.
20 – COMO GAMIFICAR O ENSINO DA MATEMÁTICA? (Sábado)
Rafael Leite, Leandro Nascimento e Pedro Passos.
O minicurso “Como Gamificar o Ensino da Matemática?” pretende apresentar de forma prática a parte conceitual e aplicada de uma estrutura gamificada. Serão mostradas diversas possibilidades
de aplicação através de “cases” que já vem fazendo sucesso entre os professores do Ensino Fundamental, Médio e Superior. Os cursistas poderão verificar a utilização de instrumentos analógicos e digitais, aprendendo suas criações, funcionalidades, vantagens e desvantagens para possíveis situações, nas quais já vivenciamos ou já recebemos o feedback de outros professores que já aplicam a metodologia.
21 – FRAÇÕES NO ENSINO FUNDAMENTAL: A PROPOSTA DO “LIVRO ABERTO DE MATEMÁTICA” (Sábado)
Letícia Rangel, Humberto Bortolossi, Victor Giraldo, Wanderley Rezende, Cydara Ripoll, Wellerson Silva e Fábio Simas.
Nesta oficina, pretendemos reproduzir parte da dinâmica de interação com professores que têm aplicado e avaliado o livro Frações no Ensino Fundamental a partir da realização de atividades propostas no material. O livro compõe o projeto “Livro Aberto de Matemática” (https://www.umlivroaberto.com/wp/), uma realização do IMPA e da OBMEP, com apoio financeiro do Itaú Social, que tem como objetivo principal a produção de livros didáticos de matemática com licença aberta a partir de um trabalho colaborativo envolvendo professores universitários e da Educação Básica. O projeto é ancorado e acompanhado por pesquisa científica e por ações de formação e de desenvolvimento profissional do professor que ensina matemática. A etapa inicial do projeto objetivou a produção do livro sobre frações, tema reconhecidamente desafiador no contexto escolar, dirigido ao Ensino Fundamental I. As atividades que compõem o livro, e que dinamizarão a oficina, são próprias para a sala de aula da Educação Básica, mas a discussão e a abordagem pretendidas visam ao professor, ao conhecimento de matemática para o ensino. A oficina é dirigida a professores que atuam nos anos iniciais (1º a 5º anos) e intermediários (6º e 7º anos) do Ensino Fundamental.
23 – PROBABILIDADE NO ENSINO MÉDIO (Sexta-feira)
Alexandre Silva, Flávia Landim, Nei Rocha, Vanessa Leal
A vida de todo cidadão é impactada por situações que exigem a tomada de decisão sujeita à incertezas presentes tanto no cotidiano, quanto em descobertas científicas. Além disso, o conhecimento probabilístico é fundamental para um aprimoramento de noções de aleatoriedade já internalizadas pelo indivíduo. Nesta oficina serão trabalhadas as atividades propostas na unidade de probabilidade do projeto Livro Aberto de Matemática para o Ensino Médio. Nessa proposta, as atividades são apresentadas de modo a motivar a introdução do conteúdo a ser trabalhado. A abordagem tradicional costuma restringir o ensino de probabilidade à interpretação clássica, definindo-a como a razão de número de casos favoráveis sobre número de casos possíveis. No entanto, a maior parte dos problemas que envolvem modelagem de fenômenos aleatórios não se encaixa nessa interpretação. Nesse material, parte do Projeto “Livro Aberto de Matemática” (http://umlivroaberto.org), uma iniciativa da OBMEP e do IMPA, com distribuição livre sob a licença Creative Commons BY-SA1, serão exploradas outras interpretações de probabilidade.
24 – ESTATÍSTICA E PROBABILIDADE NO ENSINO FUNDAMENTAL: UMA BORDAGEM INTEGRADA E INTERDISCIPLINAR (Sábado)
Flávia Landim, Leticia Rangel, Igor Melo, Vanessa Leal, Luiz Felipe Lins, Mônica Ayres, Raquel Medina, Rita Meirelles, Sandra Moreira e Camila Sajnin
Este minicurso tem como foco o ensino de Probabilidade e Estatística no Ensino Fundamental em acordo com a BNCC e considerando aspectos recomendados pela Educação Estatística e pela Associação Brasileira de Estatística. Inicialmente será realizada uma discussão crítica sobre os objetos do conhecimento da unidade temática Probabilidade e Estatística na BNCC visando ao letramento estatístico. Na sequência serão apresentadas atividades que compõem uma proposta para trabalhar de forma integrada habilidades correspondentes a essa unidade temática no sexto ano do Ensino Fundamental. Reconhecendo que a abordagem de Probabilidade e Estatística objetivando o letramento estatístico ainda é um desafio na formação e na prática do professor, o foco no sexto ano se justifica por este ano marcar uma etapa de transição. A interdisciplinaridade estará presente nessa proposta, pois os contextos a serem explorados são escolhidos a partir de habilidades da BNCC de Ciências da Natureza e Ciências Humanas.
25 – AUTENTICIDADE DE PROBLEMAS DE MATEMÁTICA (Sexta-feira)
Matheus Freitas de Oliveira, Stella Diniz de Oliveira e Fabio Simas
A relevância dos problemas de Matemática para o ensino dessa disciplina é reconhecida na comunidade científica e ratificada em diversos documentos oficiais. Contudo, o uso de problemas envolvendo situações pouco autênticas pode levar o estudante a crer que a Matemática diz respeito apenas ao cotidiano escolar. Em Palm (2009), o autor introduz aspectos que devem ser considerados para se determinar a autenticidade de um problema. Em Chamoso et al. (2013) , os aspectos de Palm são usados para se criar uma sistemática de classificação de problemas de Matemática em níveis de autenticidade. Em Oliveira (2019a) e Oliveira (2019b), os autores apresentam uma proposta de adequação da classificação e uma proposta de questionário para se identificar o nível de autenticidade do problema. Neste minicurso utilizaremos dinâmicas de metodologias ativas para levar os participantes a uma reflexão crítica sobre o tema com vistas ao desenvolvimento de exercícios e de atividades autênticas. Os professores também serão convidados a retificar atividades a fim de torná-las autênticas levando em consideração os aspectos considerados relevantes na literatura.
26 – O USO DO APP INVENTOR NO ENSINO DA MATEMÁTICA (Sexta-feira)
Demetrius Gonçalves de Araújo
Este minicurso visa apresentar aos profissionais da educação e comunidade discente uma estratégia metodológica baseada na construção de aplicativos para dispositivos móveis que possuem sistema operacional Android, como meio de fixação de conceitos e definições de conteúdos matemáticos. A ferramenta usada é a plataforma MIT App Inventor, gratuita e online, mantida pelo Instituto de Tecnologia de Massachusetts (MIT), destinada à usuários com pouca ou nenhuma experiência em programação poderem construir projetos simples e funcionais, através de um método de encaixe de blocos.
27 – MÉTODO DE SINGAPURA: EXPLORANDO A REPRESENTAÇÃO PICTÓRICA NA RESOLUÇÃO DE PROBLEMAS (Sexta-feira)
Leticia Rangel, Flávia Landim, Camila Sajnin, Igor Melo, Luiz Felipe Lins, Mônica Ayres, Raquel Medina, Rita Meirelles, Sandra Moreira e Vanessa Leal.
O Projeto Fundão Matemática, visando ao desenvolvimento profissional permanente do professor e ao ensino da disciplina, atua investigando e repensando modelos e práticas de ensino de Matemática nas diferentes etapas da Educação Básica. Este minicurso reflete a investigação de um dos grupos colaborativos do Projeto Fundão sobre o Método de Singapura. Objetiva-se explorar o potencial da representação pictórica na resolução de problemas, que tem papel central no ensino de Matemática em Singapura. Recebe especial atenção o Modelo de Barras, representação simples e visual para a abordagem de problemas aritméticos e algébricos realizada a partir de uma barra retangular em que são relacionadas quantidades e operações. No minicurso, inicialmente, serão discutidos aspectos gerais sobre o Método de Singapura e sobre a resolução de problemas. Em seguida, o Modelo de Barras será explorado a partir da discussão sobre a sua aplicação em problemas típicos do Ensino Fundamental.
28 – ÁLGEBRA: PROPOSTA DA UNIDADE TEMÁTICA NA BNCC E DESAFIOS POR SUA TRAJETÓRIA AO LONGO DOS NOVE ANOS DO ENSINO FUNDAMENTAL (Sábado)
Sérgio Augusto Amaral Lopes, Marcela Luciano Vilela de Souza e Kleber Gonçalves do Nascimento
O presente minicurso tem como objetivo principal de fazer uma análise crítica de como a Unidade Temática Álgebra é tratada na BNCC e sua trajetória ao longo dos nove anos do Ensino Fundamental. Para atingir esse objetivo faremos uso das habilidades propostas para a Álgebra na Base Nacional Curricular Comum, com atividades propostas em livros didáticos aprovados pelo Plano Nacional do Livro Didático (PNLD), bem como atividades propostas em sites educacionais. E, por fim, apresentaremos o Método Pictórico para resolução de problemas, como uma estratégia que auxilia os professores do ensino fundamental a trabalhar com essa unidade temática em sala de aula.
29 – MATERIAL CONCRETO PARA O ENSINO DE NÚMEROS INTEIROS E REPRESENTAÇÃO NA RETA NUMÉRICA (Sábado)
Yuriko Yamamoto Baldin (DM-UFSCar) e Aparecida Francisco da Silva (UNESP-IBILCE)
Resumo: Este curso trabalha uma alternativa para o ensino de números inteiros, com atenção à conceituação do campo numérico dos números inteiros, à estrutura algébrica das operações, e à representação na reta numérica. Trabalhamos uma proposta pedagógica com material concreto manipulativo que permite introduzir ludicamente os conceitos fundamentais do campo de números inteiros, acessíveis para 7º ano. As atividades evitam o treinamento do procedimento usual de memorização de fórmulas e das regras dos sinais nas operações com números inteiros. A manipulação do material resgata a aritmética de números naturais dos anos iniciais, generalizando-a para o campo de números inteiros. Trabalhamos simultaneamente um material concreto que modela a reta numérica, no qual interpretamos dinamicamente a álgebra dos números inteiros por meio de coordenadas de pontos da reta.
30 – TIKZ: UMA FERRAMENTA GRÁFICA PARA O PROFESSOR DE MATEMÁTICA (Sábado)
Fabio Simas, Beatriz Cabral e Tarso Caldas
São muitos os conhecimentos necessários à formação do Professor de Matemática e aqueles de caráter técnico podem passar despercebidos durante a graduação e pós-graduação. Elaborar listas de exercícios, provas, gabaritos, cadernos didáticos e até livros didáticos podem ser grandes desafios sem o uso das ferramentas apropriadas. Em nossa experiência com a produção de material didático no projeto do Livro Aberto de Matemática1, descobrimos no TikZ uma poderosa ferramenta para todos aqueles que, de alguma forma, desenvolvem figuras para textos em matemática. Discutiremos o pacote TikZ, da linguagem LaTeX, para o desenvolvimento de figuras em matemática. O Minicurso não exige qualquer conhecimento prévio em LaTeX ou em programação e as figuras podem ser desenvolvidas e usadas fora de um arquivo em LaTeX. A dinâmica do Minicurso está organizada em problemas de Matemática, que os participantes devem resolver utilizando os comandos apresentados da linguagem. Espera-se que ao final do Minicurso, os participantes consigam criar figuras de alta qualidade para suas provas, listas de exercícios ou materiais didáticos nas áreas de geometria euclidiana plana e funções.
Os horários estão sujeitos a alterações.

























