Minicursos aceitos para o 5º Simpósio Nacional da Formação do Professor de Matemática  

Cada participante deverá escolher um Minicurso I e um Minicurso II para frequentar durante o evento. As inscrições nos minicursos são feitas pelo sistema de eventos, no perfil de cada participante. As vagas em cada minicurso são limitadas!

Clique aqui para acessar o manual de como se inscrever nos minicursos.

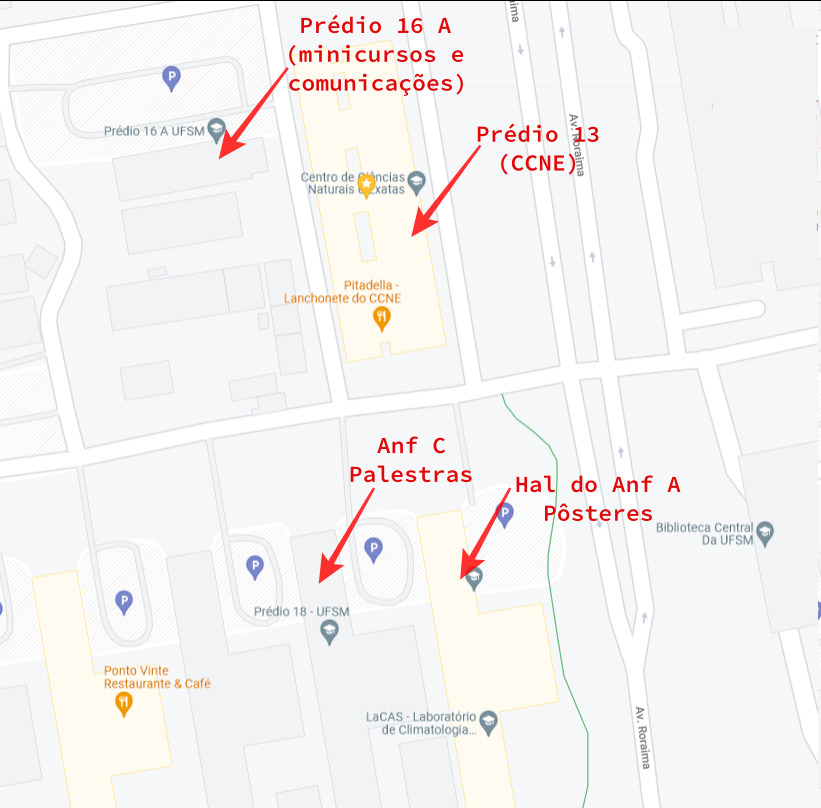
PRÉDIO 16 A – Dia 05/11 9h as 12h

PRÉDIO 16 A – Dia 05/11 14:30 – 16:00 e  16:30 – 18:00

Minicursos I – Sábado dia 05/11 – 9h às 12h

1. CRIAÇÃO DE ENREDOS DE MISTÉRIO PARA AUXILIAR O ENSINO-APRENDIZADO DE PROBABILIDADE

Mariana da Silva Costa Fernandes Vianna – Instituto Federal de Brasília (IFB)
Adriana Barbosa de Souza – Instituto Federal de Brasília (IFB)
Bruno Marx de Aquino Braga – Instituto Federal de Brasília (IFB)
Wembesom Mendes Soares – Instituto Federal de Brasília (IFB)
Evelyn Helena Nunes Silva – Instituto Federal de Brasília (IFB)

Resumo: Esta oficina pretende instrumentalizar seus(suas) participantes para a criação de histórias de mistério, adaptáveis para o formato de jogo virtual, e para sua utilização como recurso didático em processos de ensino-aprendizado de Probabilidade no Ensino Médio. Sob a perspectiva dessa pretensão, será aplicada uma metodologia de planejamento que terminará por capacitar cada cursista para: elaboração de objetivos de aprendizagem, envolvendo aleatoriedade, associados às habilidades da BNCC em Probabilidade; montagem de enredos investigativos a partir de uma estrutura narrativa básica e flexível; produção de apresentações e vídeos para, a partir de uma conta google, construir situações didáticas em plataforma online. A execução da oficina se dará pela combinação de exposição dialogada com trabalho colaborativo, nos moldes de uma aprendizagem baseada em projetos (PBL), visto que cada participante deverá concluir a formação com seu jogo digital de mistério devidamente estruturado.

2. ENCORAJANDO MENINAS PARA STEM: ATIVIDADES DE MATEMÁTICA E ROBÓTICA (A PARTIR DA EXPERIÊNCIA DO PROJETO MENINAS OLÍMPICAS DO IMPA)

Letícia Rangel – CAp/UFRJ
André Novaes – DEMAT/FEBF/UERJ e SME-RJ

Resumo: Este minicurso/oficina pretende discutir a sub-representação feminina em STEM e, em particular em matemática, a partir da experiência do projeto Meninas Olímpicas do IMPA (MOI), que que tem como objetivo primário promover a efetiva presença de alunas da Educação Básica em atividades de matemática, computação e robótica, visando a que se interessem e se sintam seguras para desenvolver carreiras nas áreas de ciência, tecnologia, engenharia e matemática (STEM). Para tal, orientados pela metodologia e pelas ações desenvolvidas no âmbito do MOI, serão propostas e discutidas atividades de matemática e robótica em Arduino.

3. PENSAMENTO COMPUTACIONAL NA EDUCAÇÃO BÁSICA: USANDO O SCRATCH PARA A CONSTRUÇÃO DE OBJETOS DE APRENDIZAGEM

Milton Kist – Universidade Federal da Fronteira Sul (UFFS)
Janice Reichert – Universidade Federal da Fronteira Sul (UFFS)

Resumo: A inserção da Computação na Educação Básica, vem ganhando cada vez mais espaço, tanto em projetos disciplinares, interdisciplinares ou em projetos de extensão (em contraturnos escolares). A Base Nacional Comum Curricular (BNCC) prevê a inclusão da Computação através de três grandes eixos: Cultura Digital, Mundo Digital e Pensamento Computacional. Em particular, o Pensamento Computacional (PC), aparece fortemente relacionado ao componente curricular de Matemática, tanto no Ensino Fundamental, quanto na área de Matemática e suas tecnologias no Ensino médio. Algumas possibilidades da inserção do PC na Educação Básica, envolvem atividades desplugadas (sem a utilização de artefatos tecnológicos), introdução a programação por meio de blocos de encaixe ou por linhas de códigos e a Robótica Educacional. O presente minicurso apresentará uma breve discussão dos fundamentos teóricos relacionados ao PC e algumas possibilidades de inclusão no componente curricular de Matemática, por fim, será utilizada a linguagem de programação em blocos Scratch para a construção de objetos de aprendizagem.

4. PLATAFORMA DE ATIVIDADES INTERATIVAS PARA A APRENDIZAGEM: LIVEWORKSHEETS

Anne Desconsi Hasselmann Bettin – Universidade Franciscana (UFN) – Santa Maria – RS
Eliane Quincozes Porto – Universidade Franciscana (UFN) – Santa Maria – RS 

Resumo: O uso de tecnologias educacionais digitais tem crescido bastante e muitos recursos têm sido disponibilizados para o professor. Nessa perspectiva, o presente minicurso tem por objetivo apresentar a plataforma Liveworksheets e suas principais funcionalidades para o desenvolvimento de atividades interativas na aprendizagem. As atividades desenvolvidas na plataforma, contemplam diferentes etapas na construção do conhecimento e podem contribuir com os professores em seu planejamento de ensino, bem como com os estudantes em diversas aprendizagens. Na busca pelo objetivo proposto, serão apresentadas a plataforma e suas especificidades, por meio de slides com o roteiro e links que encaminham para as atividades. Os participantes poderão acessar e interagir através do uso de dispositivos de uso pessoal como smartphones, tablets ou computadores. Espera-se que os participantes percebam a oportunidade de exploração da plataforma como fonte criadora e de compartilhamento, bem como uma maneira de interação na prática pedagógica. 

5. MATEMÁTICA E EDUCAÇÃO AMBIENTAL NO ENSINO FUNDAMENTAL: A CONSTRUÇÃO DE CISTERNAS E AS RELAÇÕES DE PROPORCIONALIDADE

Camila dos Reis
Fernanda Barcelos
Lidiane Buligon – Universidade Federal de Santa Maria (UFSM)
Simone Martins

Resumo: Em caráter mundial, mas principalmente no Brasil, tornam-se cada vez mais urgentes políticas públicas para conservação e preservação do meio ambiente. Pensando nisso, entende-se que a escola tem papel fundamental na educação e conscientização ambiental. Neste sentido, o presente trabalho tem por objetivo contribuir no processo de ensino e aprendizagem do conteúdo de proporcionalidade, baseado em uma proposta didática que envolve educação ambiental e matemática, a partir do estudo e da construção de cisternas. Sendo assim, propõe-se no minicurso: 

1) Apresentar um relato de experiência do projeto de ensino realizado com alunos do 9º ano de uma escola municipal de ensino fundamental da cidade de Porto Alegre. Na proposta didática foram desenvolvidos estudos históricos, teóricos, atividades práticas e de conscientização ambiental, usando como base temática a captação e reutilização da água da chuva. 

2) Apresentar maquetes de cisternas produzidas com diferentes materiais recicláveis. 

3) Reproduzir a atividade teórica-prática com os participantes a partir do estudo das relações de proporcionalidades e fatores de escalas existentes entre a construção de cisternas e a quantidade de água da chuva captada. 

Espera-se como resultado deste minicurso, que os profissionais da educação participantes possam ampliar suas ferramentas no ensino da matemática, proporcionando ao seu aluno a transposição dos saberes escolares para sua vida cotidiana, contribuindo para a formação de uma visão ampliada, crítica e contextualizada da realidade.

 6. ÁBACO VIRTUAL E ÁBACO FÍSICO DOS NÚMEROS INTEIROS: PROPOSTAS PARA A SALA DE AULA

Franciele Marciane Meinerz – EMEF Heitor Villa Lobos e Colégio Província de São Pedro
Luísa Rodriguez Doering – Universidade Federal do Rio Grande do Sul (UFRGS)
Cydara Cavedon Rippol- Universidade Federal do Rio Grande do Sul (UFRGS)

Resumo: Neste minicurso serão apresentadas as ferramentas Ábaco (físico) dos Números Inteiros e Ábaco Virtual dos Números Inteiros, este último viável para aulas remotas e presenciais, com as quais é possível abordar as operações de adição, subtração e multiplicação de números inteiros, desafiando os estudantes a refletir, a criar conjecturas, a descobrir e a deduzir as chamadas regras de sinais dessas operações. Pretende-se discutir com os participantes propostas que oportunizem esses desafios e avaliar as potencialidades de cada uma das ferramentas, incluindo sua inserção na sala de aula. Grande parte do minicurso é apoiado no ebook “O Ábaco Virtual dos Números Inteiros: um recurso para o ensino presencial e remoto” (MEINERZ; DOERING; RIPOLL, 2022).

7. LOGARITMOS E A FUNÇÃO LOGARÍTIMICA: UMA PROPOSTA NO PROJETO LIVRO ABERTO DE MATEMÁTICA

Márcio Rostirolla Adames – Universidade Tecnológica Federal do Paraná (UTFPR)

Resumo: O projeto Livro Aberto de Matemática, promovido pelo IMPA e que contou com patrocínio da fundação Itaú Social, é um esforço de professores das universidades e das escolas básicas para produzir, de maneira colaborativa, livros didáticos de matemática com excelência acadêmica e licença aberta. O projeto já conta muitos materiais para o ensino médio, sendo um deles o material sobre logaritmos e a função logarítmica. O minicurso propõe apresentar brevemente a metodologia do projeto livro aberto, discutir os resultados encontrados na pesquisa em educação sobre o ensino de logaritmos e apresentar o material, realizando algumas atividades selecionadas com os participantes.

8. GEOMETRIA NÃO EUCLIDIANA NA EDUCAÇÃO BÁSICA: UMA ABORDAGEM PRÁTICA, TECNOLÓGICA E INTERDISCIPLINAR

Claudio Iavorski – Instituto Federal do Paraná (IFPR) – Telêmaco Borba-PR
Lucas dos Santos Maciel – Colégio Marista Roque – Cachoeira do Sul-RS
Marlon Mülhbauer – Instituto Federal de Santa Catarina (IFSC) – Canoinhas-SC

Resumo: Este minicurso tem objetivo principal de propor a introdução do conteúdo de geometrias não euclidianas nos ensinos fundamental II e médio. Serão retomados alguns tópicos de história da matemática, conceitos de álgebra vetorial e trigonometria. Também serão propostas atividades com material concreto para melhor compreensão dos conceitos, identificando semelhanças e diferenças entre a geometria euclidiana e as geometrias não euclidianas. A interdisciplinaridade com a disciplina de geografia estará presente, quando se associam as definições e propriedades de geometria esférica com cartografia. Além disso, será disponibilizada aos participantes uma sequência didática para aplicar com seus alunos, com lista de exercícios, atividades práticas, uso da calculadora científica, planilhas para aprofundar o aprendizado e software de geometria dinâmica, obtendo dois resultados importantes: a determinação da menor distância entre dois pontos de uma esfera e uma propriedade relativa à soma dos ângulos internos de um triângulo esférico.

9. UNIDADES DE ENSINO POTENCIALMENTE SIGNIFICATIVAS (UEPS) PARA APRENDIZAGEM SIGNIFICATIVA NA ESCOLA BÁSICA

Mariza Camargo – Universidade Federal de Santa Maria – (UFSM)
Felipe Mendes – Universidade Federal de Santa Maria (UFSM)
Maria Cecília Pereira Santarosa – Universidade Federal de Santa Maria (UFSM)

 Resumo: Este minicurso tem como objetivo difundir para os professores de matemática da Escola Básica os pressupostos teóricos que fundamentam a elaboração de uma Unidade de Ensino Potencialmente Significativa (UEPS) como sequência didática promovedora da Aprendizagem Significativa. Será desenvolvido em um encontro de três horas, e nele serão apresentados os pressupostos teóricos da Teoria da Aprendizagem Significativa, os passos necessários para a elaboração de uma UEPS, análise de exemplos de UEPS construídos para o ensino de matemática e a proposição de elaboração de uma UEPS envolvendo conteúdos matemáticos para implementação em escolas de Educação Básica.

10. ASPECTOS CATALISADORES PARA REFLEXÃO SOBRE ATIVIDADES MATEMÁTICAS E A PRÁTICA DOCENTE

Rita Santos Guimarães – IMECC – Unicamp

Resumo: Nesta oficina serão apresentados oito aspectos que foram selecionados pela autora deste texto para servirem de guias nas discussões durante uma disciplina da licenciatura em matemática na Universidade Estadual de Campinas. Durante o semestre, a docente apresentava atividades com conteúdos do Ensino Médio e, depois da resolução da mesma pelos futuros professores, discutia-se as soluções da turma. Na sequência, a docente guiava a discussão para aspectos da atividade, focados em práticas de sala de aula, ou seja, trocava-se a lente pela qual olhávamos a atividade, inicialmente como alnos e depois como professores. Os oito aspectos foram selecionados de forma que permitissem que os licenciandos refletissem sobre a profissão, considerando tando o conteúdo matemático quanto a prática de sala de aula. Os aspectos são: Motivação inicial; Intencionalidade; Arbitrário e necessário; Atividade rica; Erros, dificuldades e preconcepções; Formas de representação; Localização do conteúdo; e Flexibilidade. Esses itens vieram de uma compilação de diversas pesquisas sobre formação de professores realizada pela autora. Nesta oficina, para ilustrar a potencialidade dos aspectos em termos de gerar reflexão sobre a prática docente, serão aplicadas pequenas atividades de introdução para as quais os participantes serão convidados a resolver e compartilhar suas impressões. Em formato de discussão guiada, serão apresentados todos os aspectos. Por fim, uma nova atividade será sugerida e os participantes, em grupos menores, serão convidados a refletir sobre alguns aspectos e a trocarem observações com outro grupo que considerou os mesmos itens. Com isso, espera-se que a oficina atinja o objetivo de sugerir uma lista coesa de aspectos que catalisam as reflexões e as discussões em torno de atividades de matemática, seja em ambientes de formação inicial de professores, em sessões de formação continuada ou no planejamento de aulas.

Minicursos II – Sábado 5/11 – 14:30 às 16h (Parte 1) e 17h às 18:30 (Parte 2)

 11. UM JOGO DE ARITMÉTICA TRABALHADO COM METODOLOGIA DE RESOLUÇÃO DE PROBLEMAS

Yuriko Yamamoto Baldin – Universidade Federal de São Carlos (UFSCar)

Resumo: O uso de jogos para atrair interesse de alunos e professores para a Matemática é conhecido e aceito por muitos professores, educadores e pesquisadores, tanto sob perspectiva cultural do desenvolvimento de pensamento matemático notada ao longo dos tempos, como também pelas recomendações curriculares das tendências educacionais atuais. A proposta desta oficina é trabalhar atividades práticas de interação dinâmica na resolução de um desafio clássico de aritmética, encontrado frequentemente em livros de jogos ou de divertimentos matemáticos, com uso sistemático da Metodologia de Resolução de Problemas. Pretende-se vivenciar as dimensões pedagógicas de situações do jogo, das quais fazem parte a descoberta, a exploração e a formulação de conjeturas, a expansão de ideias, e acima de tudo a sistematização das descobertas e das respostas. O problema é conhecido como “pilha triangular” e consiste em um desafio de preencher as casas dispostas como vértices ou pontos médios de um formato triangular com os dígitos estabelecidos. O nível de conhecimento requerido é do Ensino Fundamental I, sendo o diferencial da oficina a abordagem original de questionamentos para desenvolver o raciocínio por trás das diferentes soluções, apoiada pelo método de Lesson Study. Destinada aos professores futuros e em exercício, a atividade vivenciada pode ser executada diretamente numa sala de aula, o que enriquece o conjunto de recursos didáticos do professor de matemática, com destaque para os conteúdos de Matemática, explorados durante a resolução do problema, identificados no currículo escolar. A oficina fez parte da capacitação de professores da Diretoria de Ensino-Região de Jales, em 2021 e foi apresentada para um público majoritário de licenciandos na X Bienal da SBM, em junho de 2022.

12. CRIAÇÃO DE ROTEIROS DIDÁTICOS PARA IMPLEMENTAÇÃO DA EDUCAÇÃO FINANCEIRA NA EDUCAÇÃO BÁSICA

Aline Guedes – Universidade do Estado do Rio de Janeiro (UERJ)
Leandro Machado – Instituto de Aplicação Fernando Rodrigues da Silveira – (CAp-UERJ)

Resumo: Apresentamos nesse trabalho nossa proposta de Oficina para o 5º Simpósio Nacional da Formação do Professor de Matemática. O objetivo é trabalhar a implementação da Educação Financeira via roteiros didáticos na Educação Básica. O minicurso se dará em duas sessões de uma hora e trinta minutos cada. Na primeira, situaremos o panorama atual da Educação Financeira nas escolas, as competências esperadas pela BNCC, apresentando os principais conceitos que envolvem essa temática, além da explanação sobre a importância da criação de roteiros didáticos. Será desenvolvida a criação de um exemplo de roteiro didático com alguns dos recursos indicados selecionados, que possibilitem trabalhar com o tema “De onde vem o dinheiro?” Na segunda, os professores serão encorajados a construírem roteiros didáticos baseados na experiência da sessão anterior, utilizando os recursos indicados e problemas de investigação. Ao final, espera-se que discutamos sobre a importância da Educação Financeira nas escolas e da relevância da utilização de roteiros didáticos.

13. DEMONSTRAÇÕES VISUAIS COMO ESTRATÉGIA PEDAGÓGICA PARA O ENSINO-APRENDIZAGEM DA MATEMÁTICA

Rubens Vilhena Fonseca – Universidade do Estado do Pará (UEPA)
Dorival Lobato Jr. – Universidade do Estado do Pará (UEPA)
Antônio Sérgio dos Santos Oliveira – Universidade do Estado do Pará (UEPA)

Resumo: O presente artigo se refere à apresentação de um minicurso que se enquadra no eixo temático sobre abordagens e metodologias inovadoras em Matemática na Educação Básica e tem por objetivo oferecer uma discussão, no âmbito da Escola Básica, sobre o Infinito e as contradições decorrentes de sua natureza. Em particular, na Teoria dos Conjuntos, a noção de “equivalência de um conjunto a um de seus subconjuntos adequados” causa problemas perceptivos. Os futuros professores de Matemática geralmente não têm acesso a uma leitura elementar sobre o assunto e experimentam possíveis dificuldades em textos mais formais. A infinitude do Conjunto dos Inteiros e Racionais e a existência de Números Irracionais são assuntos do Ensino Fundamental, logo os professores devem ter uma boa compreensão deles. O objetivo deste minicurso é mostrar os efeitos que uma apresentação com provas visuais de conceitos profundos da Teoria dos Conjuntos pode desempenhar sobre as práticas dos professores de Matemática em conexão com a Base Nacional Curricular Comum (BNCC). Como o conceito de Infinito pode ser bastante contraintuitivo, apresentamos o paradoxo conhecido como Hotel de Hilbert para discutir o conceito de cardinalidade e, usando a linguagem dos videogames, apresentamos uma espiral, em que uma espécie de Pac-Man vai capturando e listando todos os números Racionais, levando a conclusão de que os Racionais são enumeráveis. Nessa perspectiva, expomos um tipo de “serpente de números” que não pode estar no Conjunto dos Racionais, levando a concluir a existência dos Irracionais e discutir o fato dos números Reais x, no intervalo 0<𝑥<1, não serem enumeráveis.

14. RELAÇÕES ENTRE MÚSICA E CONJUNTOS NUMÉRICOS

Bruno Marx de Aquino Braga – Instituto Federal de Brasília (IFB)
Evelyn Helena Nunes Silva – Instituto Federal de Brasília (IFB)
Carla Lima Santos –  Instituto Federal de Brasília (IFB)
Wembesom Mendes Soares – Instituto Federal de Brasília (IFB)
Adriana Barbosa de Souza – Instituto Federal de Brasília (IFB)

Resumo: A proposta da oficina é a de instrumentalizar seus (suas) participantes para a o ensino de conjuntos numéricos utilizando para tal as relações de frequências e divisões de escalas musicais sob a perspectiva da Teoria das Situações Didáticas. Será aplicada uma metodologia de planejamento de sequências didáticas as quais exploram habilidades da BNCC nas áreas temáticas de Números e Álgebra, as quais podem ser aplicadas a educandos de ensino fundamental II e ensino médio. A execução da oficina se dará pela combinação de exposição dialogada com trabalho colaborativo, e ferramentas da plataforma Geogebra, para que, ao fim, seus (suas) participantes possam selecionar quais elementos das sequências didáticas podem ser utilizadas em sua prática didática. 

15. MUSEU DA MATEMÁTICA UFMG: DIVERTIMENTOS GEOMÉTRICOS

Carmen Rosa Giraldo Vergara – Universidade Federal de Minas Gerais (UFMG)

Resumo: Neste minicurso serão apresentaremos atividades de Matemática Recreativa ofertadas no Museu da Matemática da UFMG e que podem ser usadas por professores dos Ensinos Fundamental e Médio. Mas especificamente, serão apresentados itens e atividades que fazem parte do acervo do Museu e daremos orientações para sua aplicação em sala de aula. Pretendemos com isto proporcionar a possibilidade de experimentar diversos recursos promotores de uma visão positiva do ensino-aprendizagem da Geometria.

16. PENSAMENTO COMPUTACIONAL PARA PROFESSORES DE MATEMÁTICA E UM MATERIAL PARA A SALA DE AULA

Leonardo Barichello – Instituto Federal de São Paulo (IFSP)

Resumo: Este minicurso vai tratar do tema pensamento computacional para professores de Matemática do Ensino Médio a partir do material publicado pelo Projeto Livro Aberto de Matemática, que traz uma abordagem alinhada à BNCC enfatizando o desenvolvimento do pensamento computacional a partir da programação de computadores. A oficina irá tratar da concepção de pensamento computacional que fundamentou o desenvolvimento do material e também apresentar, resolver e discutir algumas atividades propostas por ele com apoio de computadores, notebooks ou celulares.

17. EXPLORANDO O USO DE RECURSOS COMO TEMA PARA A FORMAÇÃO DE PROFESSORES DE MATEMÁTICA

Elion Souza da Silva – Instituto Federal do Ceará (IFCE)

Resumo: O debate sobre a natureza e a utilização de Recursos na sala de aula e no dia a dia da profissão docente tem ganhado muito espaço e valor nas comunidades educacionais nas últimas décadas, especialmente quando essa discussão se volta às esferas do ensino de matemática e dos recursos de natureza tecnológica, como computadores, smartphones, tablets etc. Dentro deste panorama, trazemos à tona uma perspectiva alternativa para este debate: Um olhar, não para o recurso em si, mas para como nossos professores os têm utilizado. Em nosso entendimento, balizado por reflexões sobre as contribuições de diversos pesquisadores acerca do tema, tão (ou mais) importante do que decidir se determinado recurso é ou não utilizável em sala de aula, é refletir sobre como este recurso pode ser utilizado, de modo que tal reflexão se manifeste a partir da compreensão de aspectos teóricos e práticos, com vistas à maximização da eficácia dessa utilização. Neste minicurso, examinaremos e discutiremos os recursos e o seu uso na matemática escolar. Trabalharemos fundamentados nos conceitos de matemática escolar como uma prática híbrida (ADLER, 2000) e na transparência dos recursos utilizados (LAVE, WENGER, 1991; ADLER, 2000). A atividade será dividida em três momentos:

• discussão sobre os conceitos de matemática escolar híbrida e de transparência, e suas implicações no uso de recursos nas aulas;
• (ii) dividiremos os professores em grupos, e cada grupo discutirá internamente três exemplos práticos de recursos-em-uso; e
• (iii) culminância das reflexões dos grupos e avaliação.

O cerne de nossa proposta é ajudar o professor de matemática a refletir a partir dessa perspectiva, através de discussões e atividades em grupo, a fim de ressignificar sua prática, e assim consiga utilizar de modo autônomo e eficiente os bastantes recursos didáticos, tecnológicos, culturais etc que acredite ser útil para a aprendizagem de seus alunos.

18. O USO DE DOBRADURAS EM PAPEL NA CONFECÇÃO DE JOGOS DE ALINHAMENTO: JOGO SHISIMA E JOGO MOINHO

Erenilda da Conceição Abuquerque – Seduc – AL e Semed – AL
Nickson Deyvis da Silva Correia – Universidade Federal de Alagoas (UFAL)
Viviane de Oliveira Santos – Universidade Federal de Alagoas (UFAL)
Tayná Elias dos Santos – Universidade Federal de Alagoas (UFAL)
Sarah Rafaely dos Santos – Universidade Federal de Alagoas (UFAL)

Resumo: A oficina intitulada “O uso de dobraduras em papel na confecção de jogos de alinhamento: Jogo Shisima e Jogo Moinho” é resultado da criação e aplicação de alguns materiais didáticos desenvolvidas no projeto de extensão “Sem mais nem menos on-line” do Instituto de Matemática da Universidade Federal de Alagoas (Ufal). Os materiais didáticos são: “Shisima – o jogo africano e a geometria”, atividade que tem como objetivo construir o tabuleiro do jogo Shisima e trabalhar a matemática presente no jogo, abordando noções básicas de geometria plana como figuras geométricas e seus elementos, tratando alguns aspectos da cultura africana que permeiam a história do jogo e trabalhando o raciocínio lógico durante o desenvolvimento das estratégias e execução do jogo; e “Jogo Moinho (trilha) – trabalhando matemática com jogo de alinhamento”, atividade que tem como objetivo trabalhar conceitos básicos da geometria, da aritmética e raciocínio lógico por meio da construção do tabuleiro e execução do Jogo Moinho. O intuito desse minicurso é motivar professores e futuros professores a construir os jogos de alinhamento Jogo Shisima e Jogo Moinho, e até propor novas ideias de atividades relacionadas com esses temas. Desta forma, iremos apresentar os materiais didáticos já desenvolvidos e aplicadas em escolas de modo virtual, posteriormente, os participantes construirão seus próprios materiais didáticos. Esperamos que esta oficina possa trazer um ganho para os participantes no que diz respeito ao contato com outras possibilidades para o ensino e aprendizagem em matemática.

19. INVESTIGAÇÃO ESTATÍSTICA NO ENSINO FUNDAMENTAL: USO DE PLANILHAS ELETRÔNICAS

Letícia Rangel – CAp/UFRJ
André Novaes – DEMAT/FEBF/UERJ e SME-RJ
Maria Helena Monteiro Mendes Baccar – Colégio Pedro II e PEMAT/UFRJ
Vanessa Matos Leal – SME-RJ e PEMAT/UFRJ
Flávia Landim – DME/IM/UFRJ

 Resumo: Esta oficina visa ao desenvolvimento do letramento estatístico no Ensino Fundamental, considerando a Base Nacional Comum Curricular (BNCC), as recomendações da Associação Brasileira de Estatística (ABE) e as Diretrizes para Ensino e Avaliação da Educação Estatística (GAISE, sigla em inglês) propostas pelo Conselho Nacional de Professores de Matemática americano (NCTM). A oficina está organizada em duas partes. Na primeira, discutiremos aspectos da BNCC com foco nas recomendações da ABE e do GAISE para o ensino da Estatística na Educação Básica. Nessa discussão, tendo como base uma atividade didática para a sala de aula, ganha ênfase o processo de resolução de problemas de investigação estatística, cuja estrutura prevê quatro etapas inter-relacionadas: formulação de questão investigativa, coleta de dados, análise dos dados e interpretação dos resultados. Na segunda parte da oficina trabalharemos a etapa análise de dados da pesquisa realizada, tendo como suporte planilhas eletrônicas. Apresentaremos exemplos de aplicações, usando o Google planilha e o Excel.

20. SISTEMAS DE NUMERAÇÃO EM UMA ABORDAGEM PROBLEMATIZADA

Victor Augusto Giraldo – Universidade Federal do Rio de Janeiro – UFRJ
Antonio Cardoso do Amaral – Fundação de Amparo à Pesquisa do Estado do Piauí/FAPEPI

Resumo:O conceito de número natural nasce na ideia concreta de contagem e se generaliza na noção de correspondência um a um entre objetos de dois conjuntos. Um número natural é a expressão abstrata de uma quantidade. No contexto da existência de representações com símbolos, chamados numerais, com características próprias de representação de quantidades inteiras, surgem os Sistemas de Numeração. Este trabalho organiza uma apresentação dos Sistemas de Numeração e busca privilegiar o debate teórico em torno das estruturas algébricas que os compõem. Nessa abordagem, teremos a oportunidade de revisitar formas de contar e registrar quantidades usadas pelos povos antigos e suas contribuições para o surgimento de Sistemas de Numeração mais adequados às necessidades do seu tempo. Discutiremos as diferentes representações para uma mesma quantidade (mudanças de base), incluindo a realização de operações aritméticas e propriedades dos números, como divisibilidade e resto.

————————————————————————————————————————————————————————————————————-

Os minicursos/oficinas terão duração total de 3 horas, podendo ser divididos em dois momentos, ministrados na modalidade presencial que tratarão de assuntos condizentes com algum dos eixos temáticos (apresentados abaixo) propostos pelo evento.

O minicurso/oficina deve ter no máximo 5 (cinco) autores devidamente inscritos no evento e com as inscrições confirmadas ao ser submetido e avaliado pela comissão avaliadora.

Não serão disponibilizados materiais impressos para a realização dos minicursos.

Caso os autores desejarem disponibilizar algum material para os participantes de seu minicurso, este deverá ser enviado para o e-mail da submissão com até uma semana antes do evento.

Para a submissão de propostas é necessário seguir o template disponibilizado e enviá-lo em formato .pdf para o e-mail submissao.simposio.anpmat@gmail.com de 15 de Junho de 2022 a 15 de Agosto de 2022. PRORROGADO ATÉ 22/08.

ATENÇÃO: A inscrição pode levar até 3 dias para a confirmação no sistema, uma vez que depende do retorno bancário sobre a informação de pagamento, por isso, não deixe para realizar a inscrição no dia da submissão da sua proposta. Em hipótese alguma serão recebidas propostas de minicursos fora do prazo de envio.

O arquivo do resumo deverá ser salvo com o nome: MC_eixo temático_nome do autor_último sobrenome.pdf

Exemplo: MC_T2_Maria_Silva.pdf.

Clique aqui para baixar o modelo para submissão de minicursos/oficinas.

Eixos Temáticos

T1: Abordagens e metodologias inovadoras em Matemática na Educação Básica
T2: Ensino de Matemática nos anos iniciais (1º a 5º) do Ensino Fundamental
T3: Ensino de Matemática no ensino Fundamental II (6º ao 9º ano) e Ensino Médio.
T4: Ensino de Matemática na Educação de Jovens e Adultos e nos cursos técnicos integrados ao Ensino Médio
T5: Formação inicial e continuada de professores de Matemática
T6: Desenvolvimento de materiais e recursos didáticos de Matemática
T7: Tecnologias digitais no ensino de Matemática
T8: Avaliação no ensino de Matemática
T9: História da Matemática e prática docente
T10: Educação Inclusiva e Matemática

Para realizar sua inscrição acesse http://eventos.anpmat.org.br

Acesse https://associados.anpmat.org.br e associe-se a ANPMat!

Associados à ANPMat têm desconto de 25% na inscrição deste e todos os simpósios organizados pela ANPMat.

Cada participante deverá escolher dois minicursos.