
Você já ouviu falar sobre a Lei de Benford? Já pensou em abordar este tema em sala de aula?
A Lei de Benford faz parte de um grupo de surpreendentes descobertas matemáticas de caráter contraintuitivo, cuja descoberta contou com elementos do acaso e que acabou se transformando numa poderosa ferramenta de combate a fraudes. Além dessas, outras características tornam este tema rico para exploração em sala de aula, como por exemplo, suas surpreendentes propriedades matemáticas.
O astrônomo Simon Newcomb foi o primeiro a observar que, em grandes conjuntos de números das mais variadas naturezas, o algarismo 1 aparece na primeira posição significativa com maior frequência que o 2, que por sua vez é mais frequente que o 3 e assim sucessivamente.
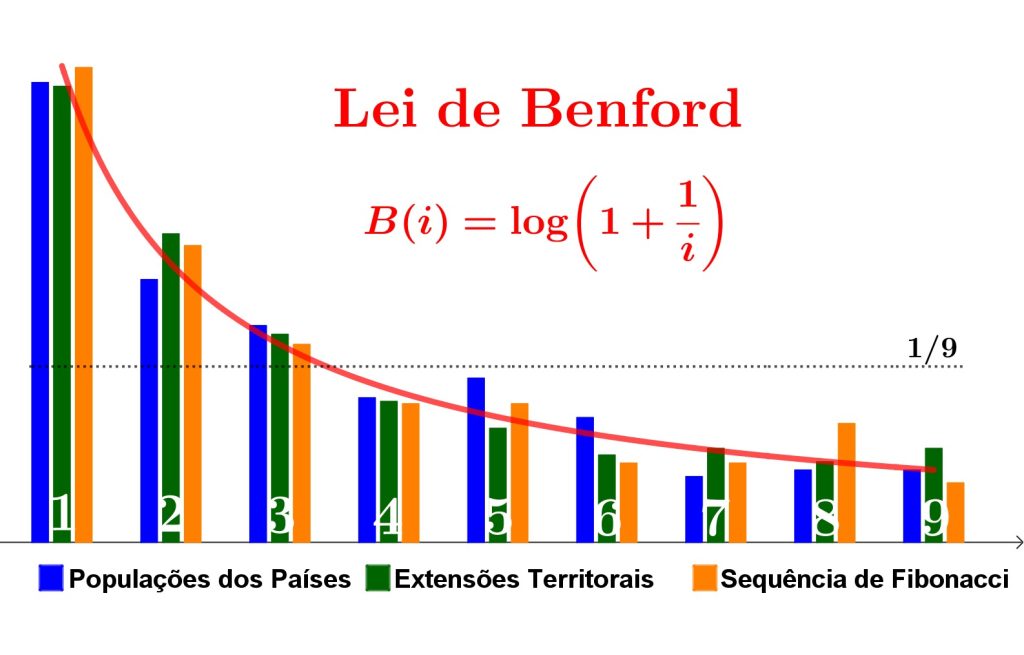
Ele notou este fenômeno ao observar que, nas extensas tábuas de logaritmo utilizadas na época, as páginas correspondentes aos algarismos menores estavam mais gastas que as dos algarismos maiores. Então ele propôs a seguinte lei para a distribuição de probabilidades dos algarismos:
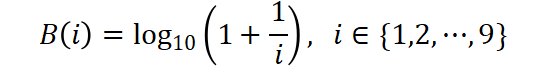
Este achado, que ficou esquecido no tempo, foi redescoberto anos depois pelo físico Frank Benford, que, além de promover sua divulgação, desenvolveu generalizações e realizou testes do funcionamento da Lei em imensos conjuntos numéricos de diversas origens. Hoje sabemos que ela se aplica a incontáveis tipos de conjuntos de dados, como listas de comprimentos de rios, populações, extensões territoriais, balancetes contábeis entre muitos outros.
Novas descobertas foram feitas com o passar do tempo, como leis de distribuição para os algarismos seguintes e os surpreendentes fatos de que a Lei de Benford é invariante por mudança de escala e por mudança de base. Assim, um conjunto de extensões de rios dadas em quilômetros, continuará satisfazendo esta Lei se os dados forem convertidos em milhas.
Além disso, algumas sequências numéricas matematicamente conhecidas, como a sequência das potências de 2 e a emblemática sequência de Fibonacci também satisfazem a Lei de Benford! Estes fatos surpreendentes decorrem de um teorema que afirma que o conjunto ![]() satisfaz esta Lei sempre que
satisfaz esta Lei sempre que ![]() for irracional.
for irracional.
Descobertas recentes mostraram quais características são necessárias e o porquê de a Lei de Benford se aplicar aos mais diversos conjuntos de números. Hoje, esta lei é amplamente utilizada desde o combate a fraudes em orçamentos de obras públicas à confiabilidade de sistemas eleitorais. Afinal, um conjunto de dados que não obedece a Lei de Benford merece ser alvo de um escrutínio.
Apresentação do Desafio
Você consegue pensar em como desenvolver todo este rico conteúdo em sala de aula utilizando tecnologias digitais? As possibilidades são infinitas!
Se sim, grave um vídeo de até 10 minutos no seu canal do YouTube com a sua proposta em reposta a este desafio e envie o link para ANPMat até o dia 15/10/2023 através do formulário disponível no link https://forms.gle/Zc5X5VWLrPpuEbJQA.
Seu vídeo pode ser publicado junto com o nosso vídeo-resposta oficial!
Alternativamente, deixamos também um intrigante desafio matemático sobre a Lei de Benford, cuja solução você pode nos enviar por vídeo seguindo as mesmas instruções dadas anteriormente.
Desafio Matemático
Mostre que, qualquer que seja a área inicial de um triângulo equilátero, a sequência das áreas (pintadas em preto) das figuras produzidas pelas iterações que transformam o triângulo original no triângulo de Sierpinski satisfaz a Lei de Benford.

Solução do Desafio
Assim como no Desafio 1, convidamos os professores de matemática e estudantes a apresentarem soluções para um desafio matemático relacionado ao tema, bem como apresentar uma proposta de atividade didática com o uso de tecnologias digitais. Mais abaixo, compartilhamos o resultado desta proposta.
Além das soluções que nos foram enviadas, trouxemos também nossa parcela de contribuição para a solução do desafio proposto produzindo nosso próprio vídeo-resposta e um texto ampliado com uma abordagem mais completa do tema Lei de Benford, incluindo uma sistematização dos conceitos e algumas provas das propriedades matemáticas envolvidas, bem como algumas propostas mais detalhadas de como este tema pode ser utilizado em sala de aula.
Acesse esses materiais clicando nos links abaixo.
Agora, vamos dar destaque às pessoas que contribuíram conosco, respondendo a este segundo Desafio ANPMat. É com grande satisfação que divulgamos os nomes dos autores dos vídeos enviados, bem como os links para acessá-los.
1. Bruno Rios Souza – aluno de graduação orientado pela professora Ana Carla Percontini da Paixão. O Bruno enviou dois vídeos em resposta aos desafios didático e matemático:
– Utilizou uma planilha do Excel para mostrar a validade da propriedade enunciada no desafio matemático: https://www.youtube.com/watch?v=VykjA6rewfE
– Com uma produção cheia de recursos, mostrou como abordaria este tema em sala da aula: https://www.youtube.com/watch?v=GEe1WFYSYtQ&ab_channel=BrunoRios
2. Charles Bolzanell Bosi – aluno de graduação que contou com a colaboração dos colegas Fábio Brito de Castro e Marcos Vinicius Trindade Vieira e com a orientação do professor Rubens Vilhena Fonseca. O Charles enviou um vídeo em resposta ao desafio matemático:
– Abordou diversos aspectos do problema, apresentando inclusive uma fórmula para obtenção do primeiro algarismo significativo de um número real qualquer: https://www.youtube.com/watch?v=8qH7Ib9ySFw
3. Noel José da Costa – professor do IFRJ. O Noel enviou dois vídeos em respostas aos dois desafios propostos:
– Apresentando uma aplicação desenvolvida por ele, o professor propõe atividades para o ensino de conceitos de Probabilidade por meio de exercícios e simulações, nos quais inclui uma proposta para testar a Lei de Benford: https://www.youtube.com/watch?v=SHuaSJBNNjM
– Utilizando a mesma aplicação citada no primeiro vídeo, o professor ilustra, por meio de testes, o funcionamento da lei, além de apresentar argumentos matemáticos para a validade da propriedade enunciada: https://www.youtube.com/watch?v=FPDW2ARX6aM
