Admilson Batista da Silva
Geometria Analítica Dinâmica é o resultado da dissertação de mestrado pelo PROFMAT do Prof. Admilson Batista da Silva, apresentado em 13 de novembro de 2015, na UFTM em Uberaba MG, tendo como orientador o Prof. Dr. Osmar Aléssio. A obra teve como objetivo realizar um estudo dos recursos oferecidos pelo software GeoGebra, no que diz respeito a suas aplicações no estudo da Geometria Analítica, visando um enriquecimento dos recursos pedagógicos deste conteúdo e, consequentemente, obter melhores resultados no que se refere ao processo ensino-aprendizagem. Para isso foram criadas algumas atividades dinâmicas explorando os recursos do GeoGebra. Essas atividades abordam conceitos da Geometria Analítica de forma dinâmica e interativa, facilitando, assim, a formulação desses conceitos. Não se trata de um estudo de todos os recursos e comandos do GeoGebra, mas de exemplos de atividades que podem ser desenvolvidas pelos professores, com o objetivo de aplicar recursos pedagógicos mais dinâmicos e interativos, tornando as aulas mais interessantes.
Vamos mostrar aqui algumas dessas atividades. O trabalho na íntegra pode ser visto no site do PROFMAT em: http://www.profmat-sbm.org.br/dissertacoes
Para realizar as atividades propostas a seguir, você precisará instalar o software:
Atividade 1: Condição de alinhamento de três pontos
O objetivo dessa atividade é levar o aluno a perceber, de forma dinâmica, o conceito de condição de alinhamento de três pontos, relacionando com pontos colineares e com pontos não colineares.
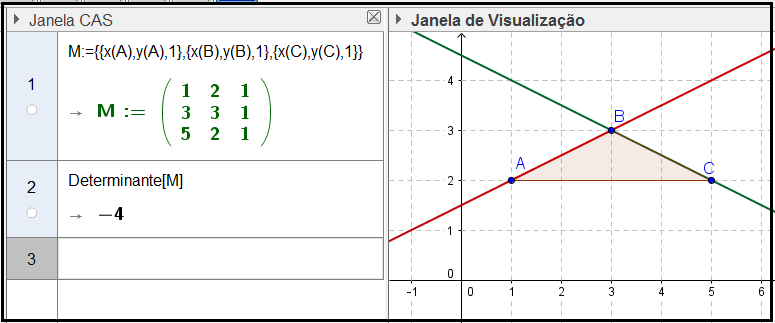
A dinâmica pode ser obtida deslocando-se os pontos A, B e C indicados na figura 1. À medida em que as coordenadas dos pontos A, B e C variam, os valores indicados na matriz e no valor do determinante também variam.
Figura 1: Atividade Condição de alinhamento de 3 pontos
Para construir essa atividade, clique aqui para seguir os passos.
Veja o arquivo da atividade dinâmica AQUI.
Atividade 2: Distância entre ponto e reta
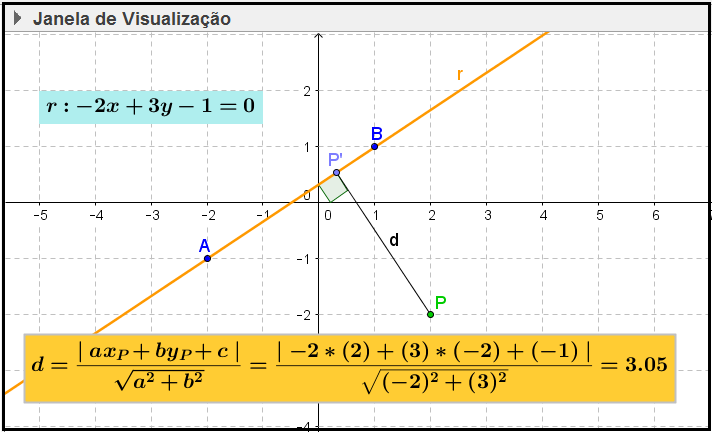
O objetivo dessa atividade é permitir que o aluno visualize, geometricamente, a distância entre um ponto P e uma reta r, e relacione essa distância com os elementos da fórmula
Figura 2: Atividade Distância entre ponto e reta
A dinâmica pode ser obtida deslocando com o mouse, os pontos A, B e P.
Para construir essa atividade, clique aqui para seguir os passos.
Veja o arquivo da atividade dinâmica aqui.
Atividade 3: Inequação do 1º grau com duas variáveis
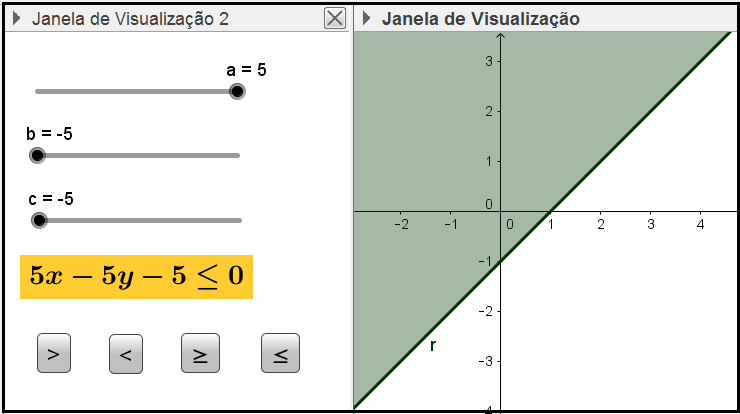
O objetivo dessa atividade é proporcionar ao aluno uma visualização gráfica do semiplano definido por uma inequação do 1º grau com duas variáveis, bem como perceber os efeitos causados pela variação dos coeficientes e dos sinais de desigualdade dessa inequação.
Figura 3: Atividade Inequação do 1º grau com duas variáveis
A dinâmica pode ser obtida deslocando os botões dos controles deslizantes para alterar os valores dos coeficientes, ou clicando sobre os botões de comando para alterar o sinal de desigualdade da inequação.
Para construir essa atividade, clique aqui para seguir os passos.
Veja o arquivo da atividade dinâmica aqui.
Atividade 4: Posições relativas entre ponto e circunferência
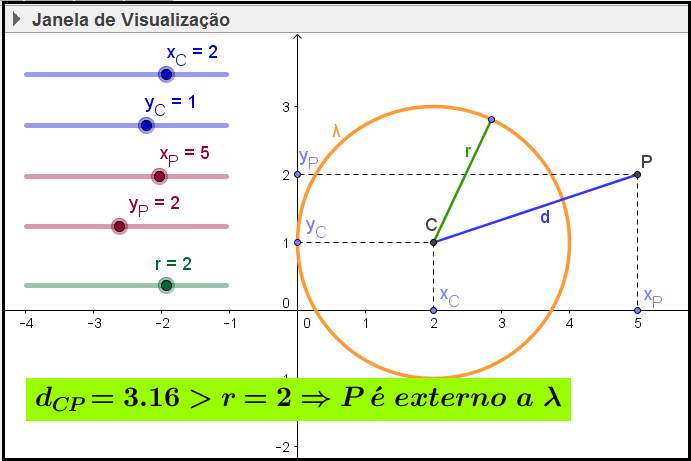
O objetivo dessa atividade é levar o aluno a perceber, através da visualização gráfica, as posições relativas entre um ponto P e uma circunferência λ, relacionando essas posições com os valores do raio da circunferência e da distância entre o centro da circunferência e o ponto P.
Figura 4: Posições relativas entre ponto e circunferência
A dinâmica pode ser obtida movimentando os botões dos controles deslizantes, ou arrastando os pontos C e P no gráfico.
Para construir essa atividade, clique aqui para seguir os passos.
Veja o arquivo da atividade dinâmica aqui.
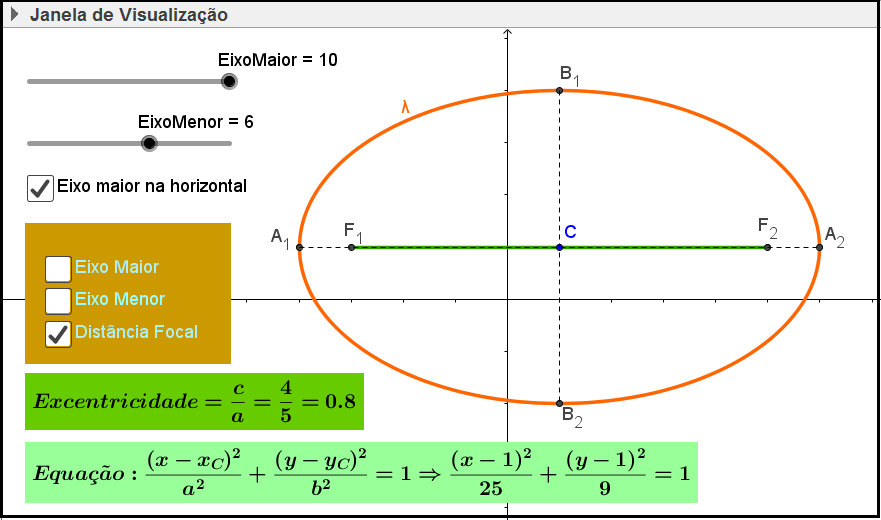
Atividade 5: Elipse
O objetivo dessa atividade é auxiliar o aluno na identificação dos elementos de uma elipse, bem como fazer com que ele perceba as variações do eixo maior, do eixo menor, da distância focal, da excentricidade e dos elementos que compõem a equação da elipse, estabelecendo relações entre essas variações e as variações do formato gráfico da elipse.
Figura 5: Atividade Elipse
Os dois controles deslizantes permitem variações do eixo maior e do eixo menor, variando, assim, a excentricidade da elipse. A programação dos controles não permite que o eixo maior assuma valores menores que o eixo menor ou que o eixo menor assuma valores maiores que o eixo maior.
A caixa Eixo maior na horizontal alterna as posições horizontal e vertical do eixo maior e do eixo menor, além de trocar a ordem dos elementos a2 e b2 na equação.
As caixas Eixo Maior, Eixo Menor e Distância Focal permitem a exibição não simultânea desses elementos no gráfico, facilitando assim, sua identificação e visualização.
Para construir essa atividade, clique aqui para seguir os passos.
Veja o arquivo da atividade dinâmica aqui.