Katia Regina Ashton Nunes
Associação Educacional Miraflores – Niterói – RJ
Que tal trabalhar muitos dos conceitos matemáticos presentes no Ensino Fundamental através do estudo e análise de obras de arte?
Esta é a minha proposta. Há anos pesquiso as relações existentes entre duas importantes áreas do conhecimento: a Matemática e a Arte, e nesse período muitos projetos foram desenvolvidos com artistas plásticos de destaque mundial. A pesquisa gerou a publicação de cinco livros: Fazendo Arte com a Matemática, Tecendo Matemática com Arte, Descobrindo Matemática na Arte, Matemática-Práticas Pedagógicas para o Ensino Médio, e o mais recente, Fazendo arte com a matemática- 2ed, que vem reformulado, e com um novo capítulo dedicado a artistas brasileiros que participaram dos Movimentos, Concretista e Neoconcretista. Eles foram publicados pela editora Artmed/ Grupo A e em todos tive o privilégio de ter como parceira a Drª Estela Kaufman Fainguelernt, minha mestre inspiradora e de uma legião de educadores matemáticos.
O ensino da Matemática centrado em si mesmo, limitando-se à exploração de conteúdos meramente acadêmicos, de forma isolada, sem qualquer conexão entre seus próprios campos ou com outras áreas de conhecimento, pouco tem contribuído para a formação integral do aluno, com vistas à conquista da cidadania. (PCN Matemática)
Minha intenção com este trabalho é fazer com que o espaço da sala de aula de Matemática se transforme num ambiente de argumentação, de pesquisa, e de construção de conhecimentos. Um espaço onde se desenvolva a diversidade de pensamento, a intuição, a imaginação, e a criatividade. E onde o professor possa assumir o papel de propositor, mediador de aprendizagens. E foi na Arte que encontrei uma grande aliada para alcançar meus objetivos.
Conhecer arte envolve o exercício conjunto do pensamento, da intuição, da sensibilidade e da imaginação (PCN Arte)
Na pesquisa, me inspirei nas ideias de Lygia Clark que revolucionou a arte brasileira e o espaço do Museu, ao se deslocar da posição de artista inteiramente responsável pela criação de uma obra para a de propositora, rompendo com a ideia de que a arte devia ser apenas contemplada. Lygia Clark criou objetos de arte que estimulavam a participação ativa do público e sua interação com a obra.
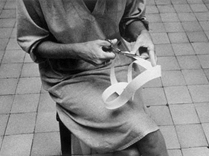
Em 1960 cria a série Bichos, que são objetos constituídos por placas de metal que se unem por meio de dobradiças, possibilitando infinitas posições quando manipulados. E em 1964, Caminhando, obra em que o participante cria uma fita de Mobius. Ao percorrê-la, o próprio participante realiza a obra de arte.

Durante a investigação ficou evidente a influência mútua de uma dessas áreas sobre a outra desde os primeiros registros históricos que temos de ambas. Muitos foram os artistas de diferentes tendências da arte que utilizaram a Matemática na elaboração de suas obras. Focando nossos olhares somente a partir do século XX, cito Picasso e o Cubismo, Mondrian e o Neoplasticismo. E ainda Max Bill, que dizia que o elemento de toda obra plástica é a Geometria, relação de posições sobre o plano e no espaço; e Escher cuja obra se impõe a qualquer estudo relacionando Matemática com Arte. Ele dizia “sinto muitas vezes que tenho mais em comum com os matemáticos do que como os meus colegas artistas”.
Os exemplos do encontro entre Matemática e Arte podem ser multiplicados enormemente.
Nesse texto relatarei, de forma bem sucinta, alguns dos muitos projetos que foram vivenciados por alunos da Associação Educacional Miraflores- Niterói, escola que atuo como Coordenadora de Matemática.
Um dos projetos envolveu obras de Luiz Sacilotto, artista brasileiro que dizia que a geometria era a sua paixão, e foi desenvolvido no 8º e 9º anos do Ensino Fundamental.
Esse importante artista foi pioneiro no âmbito da tridimensionalidade, ao desdobrar o plano no espaço. Ele também foi um dos precursores da op art no Brasil, criando uma pintura que explora fenômenos óticos, num jogo ambíguo com as formas.
Iniciamos o projeto reunindo estudos sobre a vida e obra desse artista procurando caracterizar o momento histórico, político e social de sua época. Passamos então a pesquisar o Movimento Concretista Brasileiro, do qual ele foi um dos mais fiéis representantes e pesquisar sobre outros artistas que integravam esse importante movimento. É importante destacar que no Brasil, o Concretismo penetrou não só na pintura e escultura, como também na poesia e arquitetura.


Em outra etapa do projeto, propus aos alunos a reprodução de algumas obras de Sacilotto e a criação de diferentes leituras, além da análise e construção com recortes e dobraduras de papel de duas esculturas, Concreção 5816 e Concreção 5839. Durante e após as reproduções e a construção das esculturas, muitos conceitos matemáticos foram explorados. Por exemplo, ao trabalhar com a obra Concreção 5816, de dimensões 45x45x45cm, pedi aos alunos que descobrissem qual o diâmetro e o raio do círculo que deu origem a escultura? E ainda, qual a área desse círculo? E qual o comprimento de sua circunferência?



Ao final pedi aos alunos que criassem sua própria escultura utilizando a técnica empregada por Sacilotto; dando um título a ela e registrando os conteúdos matemáticos que poderiam ser explorados a partir dela.
A culminância do projeto se deu com a montagem de uma exposição dos trabalhos realizados.
Concreção 5629 foi outra obra escolhida para este projeto. A partir dela explorei dentre outros o estudo dos triângulos, e outros polígonos, ângulos, congruência e semelhança de figuras, Teorema de Tales, perímetro, e área.

Ainda desenvolvi o projeto Simetria e Arte com alunos do 8º ano. Escolhi para o trabalho obras de Milton Dacosta, dentre elas, Figura com Chapéu. Nela foi aplicada a reflexão.

Outras obras fizeram parte do projeto, Quatro grupos de elementos e Espaço virtual, ambas de Judith Lauand, conhecida como a Dama do Concretismo. Na primeira há simetria de translação e na segunda há rotação de 60° em torno do ponto central do hexágono que figura na obra.


E ainda a obra Planos em Superfície modulada n.4 de Lygia Clark, nela há simetria de rotação de 180°(simetria central).

Dando sequência ao trabalho apresentei aos alunos, obras de Escher onde foi possível observar diferentes pavimentações. Nessas pavimentações identificamos translações, rotações, reflexões e composições dessas transformações.
Os alunos ficaram surpresos ao saber que Escher descobriu sozinho que, combinando uma ou mais isometrias é possível obter 17 tipos de mosaicos.


Após descrição/ apreciação das obras, estudo da vida e obra dos artistas e leituras das obras escolhidas para o trabalho, propus aos alunos que pesquisassem outras obras de arte que apresentassem os diferentes tipos de simetria ilustrados anteriormente. Depois, muitas atividades foram desenvolvidas com o objetivo de consolidar os conceitos e finalmente foi proposta a criação de obras utilizando cada um dos tipos de simetria estudados que podiam ser construídas com material de desenho ou ainda um software de geometria dinâmica entre eles, o Geogebra.
Outro projeto, denominado Poliedro–Arte, foi desenvolvido no 9º ano Ensino Fundamental, e focou suas pesquisas em artistas plásticos que utilizaram diferentes poliedros construção de suas obras, entre eles, Franz Weissmann, Regina Silveira, Milton Dacosta, Nelson Leirner e M. C. Escher. As obras desses artistas permitiram a exploração de conceitos como sólidos geométricos, vértices, faces, arestas, relação de Euler, vistas de objetos, planificações dos sólidos, área total, volume do cubo, os Poliedros de Platão, e planos de simetria do cubo.


Ao longo todos os projetos que já desenvolvia História, a Geografia e a Língua Portuguesa são disciplinas que se integram de modo natural ao trabalho, possibilitando assim a criação, em sala de aula, de um diálogo interdisciplinar permanente.
Para conhecer um pouco mais sobre este trabalho e descobrir como é gostoso trabalhar matemática com arte basta acessar o site www.matematicaearte.com.br
