Victor Giraldo (Instituto de Matemática / UFRJ)
victor.giraldo@ufrj.br
O livro Recursos Computacionais no Ensino de Matemática (autores: Victor Giraldo, Paulo Caetano e Francisco Mattos; edição: SBM, 2013; ISBN: 978-85-85818-67-8) foi produzido como livro texto para a disciplina de mesmo nome do PROFMAT. O objetivo do volume é apresentar ao professor de Matemática possibilidades de uso de recursos digitais na sala de aula da escola básica.
Desta forma, a ideia não é “ensinar a usar os softwares”, esgotando todas as suas possibilidades técnicas, e sim discutir potencialidades e limitações do uso de algumas ferramentas no ensino de Matemática. Isto é, o texto não é concebido como um tutorial para o uso dos programas computacionais (que o leitor não terá dificuldades de encontrar na internet). Esses softwares servem basicamente como exemplos para ilustrar a discussão sobre as atividades propostas – que é o foco principal do livro.

O texto é organizado em torno da aplicação das atividades e da discussão sobre elas, abordando principalmente os seguintes aspectos: os objetivos instrucionais das atividades, os conceitos matemáticos tratados, o papel do computador no desenvolvimento das atividades, as vantagens e as limitações da realização das atividades em sala de aula. Entretanto, o texto não é tampouco concebido como uma coleção de atividades que possam ser transportadas diretamente para a sala de aula. A ideia é que as discussões conduzidas, com base nas atividades propostas, forneçam subsídios teóricos e metodológicos para que o professor elabore suas próprias atividades, adequadas a cada contexto escolar específico. Para que este fim seja atingido, é fundamental a reflexão sobre os objetivos das atividades e, em especial, sobre o papel do computador na sua realização.
Com essa organização, objetiva-se apresentar e discutir exemplos de atividades em que as ferramentas digitais desempenhem efetivamente um papel para a aprendizagem dos conceitos matemáticos – e não sejam meros adereços para tornar mais atrativos exercícios que poderiam ser facilmente abordados apenas com papel e lápis. Portanto, objetiva-se apresentar propostas em que o uso do computador permita apresentar aspectos dos conceitos matemáticos que não poderiam ser abordados de outra forma. Isto é, um objetivo central deste livro é destacar o que o uso do computador pode acrescentar em relação à abordagem usual como lápis e papel – abrindo caminhos para novas formas de ensinar e aprender Matemática. Para ilustrar essa perspectiva do uso do computador, apresentaremos a seguir alguns exemplos extraídos do texto.
A leitura do livro também não exige conhecimentos prévios sobre o uso dos softwares, uma vez que as ferramentas vão sendo gradativamente apresentadas na medida em que são necessárias para a realização das atividades. Os capítulos são organizados por modalidades de recursos digitais, começando pelos mais simples e aumentando em sofisticação: calculadoras de bolso, ambientes gráficos, ambientes de geometria dinâmica, sistemas de computação algébrica. O livro aborda ainda ensino a distância, pesquisas eletrônicas e critérios para seleção de recursos computacionais. Essa organização visa apresentar situações em que, mesmo com recursos simples, é possível fazer explorações matemáticas interessantes.
Embora o livro tenha sido originalmente concebido para o Mestrado Profissional em Matemática em Rede Nacional, ele se destina aos mais diversos níveis de formação de professores de Matemática, como disciplinas da licenciatura, cursos de extensão, aperfeiçoamento e extensão. Sobretudo, espera-se que as discussões conduzidas no texto possam promover reflexões sobre o ensino e a aprendizagem de Matemática que extrapolem o uso dos recursos digitais e possam ser aplicadas a situações pedagógicas mais gerais.
Para realizar as atividades dos exemplos a seguir, você precisará instalar os softwares:
EXEMPLO 1: Atividade 3.25, P. 84.
Uma forma de usar o computador de forma que ele desempenhe um papel efetivo é aproveitar suas limitações técnicas como potencialidades pedagógicas. A ideia geral é empregar situações em que o software gere resultados inesperados ou aparentemente errados para motivar a investigação matemática sobre essas aparentes incoerências. Essa é a proposta da Atividade 3.25. Veja o texto da atividade aqui.
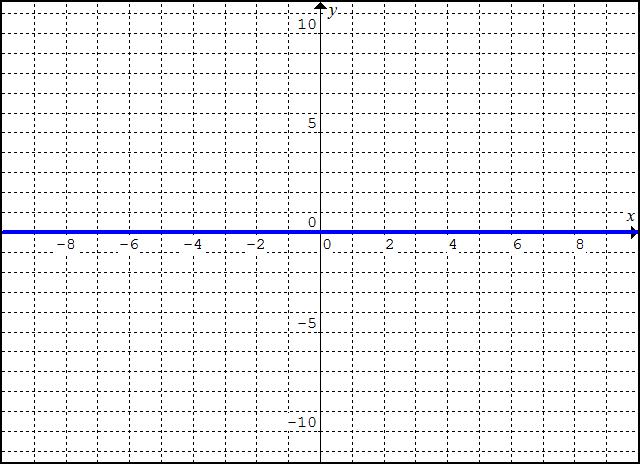
Note que, quando traçamos o gráfico de u na janela gráfica -10 ≤ x ≤ 10, -10 ≤ y ≤ 10, aparece a figura abaixo, que não corresponde à imagem esperada para o gráfico. Isto ocorre porque todos os valores de u(x) ficam contidos no intervalo 0 < y ≤ 0,001 , portanto são muito pequenos em relação à janela escolhida.
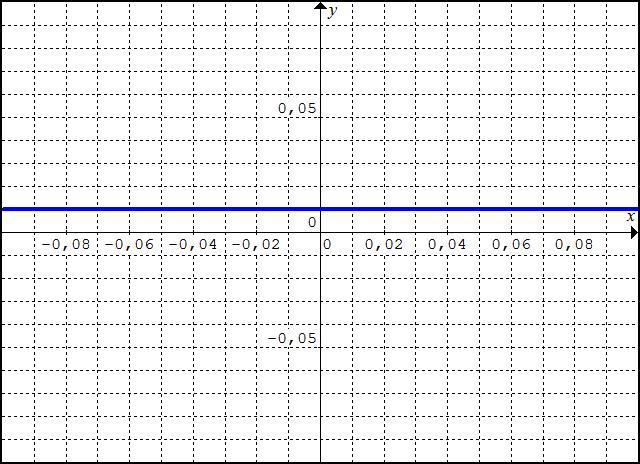
Por outro lado, quando o gráfico de u é traçado na janela -0,1 ≤ x ≤ 0,1, -0,1 ≤ y ≤ 0,1, a figura que aparece (abaixo) tampouco corresponde ao esperado para o gráfico. Note que, se x é próximo de 0, então x6 é ainda mais próximo. Portanto, no intervalo -0,1 ≤ x ≤ 0,1, os valores de u(x) = 1/(x6 + 100) ficam muito próximos de 1/100.
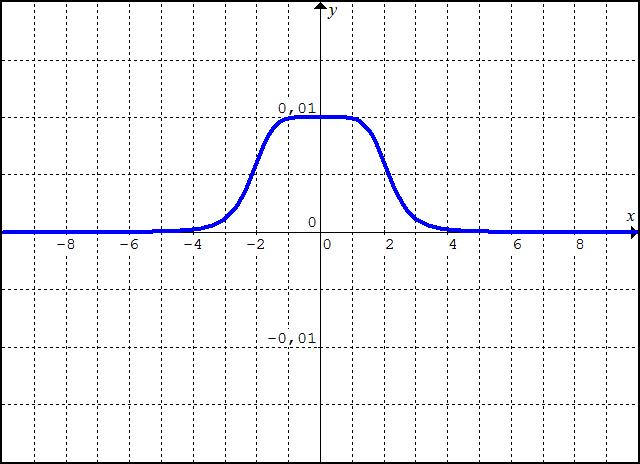
Portanto, para retratar a variação global da função, deve-se buscar uma janela gráfica com valores “grandes” para x e “pequenos” (próximos de 0) para x. O fio condutor da investigação que conduz a esta conclusão deve ser a exploração das relações entre as propriedades algébricas da função e o comportamento de seu gráfico, considerando as ordens de grandeza das variáveis em cada janela. O professor tem o importante papel de orientar os alunos nessa direção durante a realização das atividades. Esta atividade oferece uma alternativa para abordagem usual de gráficos de funções reais, que, além de envolver um repertório limitado de exemplos (basicamente funções polinomiais), segue quase que invariavelmente o esquema de substituir valores e ligar os pontos, com pouca reflexão qualitativa envolvida.
A atividade foi desenvolvida aqui com o software Graphmatica. Porém, ela pode ser feita com qualquer software simples que permita traçar gráficos a partir das expressões analíticas, e alterar janelas gráficas de visualização.
EXEMPLO 2: Atividades 4.14, p. 130-131 e e 4.21, p. 147-148.
Nos últimos anos, os ambientes de geometria dinâmica – especialmente o Geogebra – têm se constituído em importantes recursos para o ensino de Matemática em todos os níveis, desde o ensino fundamental até a universidade. Em linhas gerais, esses ambientes simulam as construções com as ferramentas euclidianas físicas régua e compasso. A diferença está no fato de que as construções feitas no software são dinâmicas, isto é, é possível mover os elementos da construção e observar as alterações nos objetos geométricos dependentes. Esse recurso oferece uma ampla variedade de possibilidades pedagógicas.
Estas atividades envolvem a construção dos círculos simultaneamente tangentes a uma reta e a um círculo dados. Em uma primeira análise, é possível alterar as posições relativas entre a reta e o círculo dados, e analisar as mudanças consequentes nos círculos tangentes construídos. Esta é a proposta da Atividade 4.14. Em um segundo nível de análise, a Atividade 4.21 propõe variar o ponto de tangência e traçar os lugares geométricos dos centros dos círculos tangentes.
Veja os textos das atividades aqui.
Veja os arquivos das atividades aqui e aqui.
É importante observar que as construções geométricas no ambiente computacional devem sempre ser acompanhadas de justificavas fundamentadas em argumentação matemática.

EXEMPLO 3: Atividade 4.32, p. 164-165.
Os ambientes de geometria dinâmica têm sido muito utilizados no ensino de geometria. Porém, eles também podem ser de grande valia para o ensino de funções. Em especial, o GeoGebra oferece a integração de ferramentas para construções geométricas com sistemas de coordenadas cartesianas e manipulação de simbologia algébrica, possibilitando abordagens articuladas para geometria sintética e geometria analítica. A proposta desta atividade é explorar essas ferramentas para a aplicação de transformações geométricas elementares (translações e dilatações) em gráficos de funções reais de uma variável real. Assim, é possível variar os parâmetros e analisar qualitativamente os efeitos nos gráficos, observando seu movimento na tela.
Veja o texto da atividade aqui.
Veja o arquivo da atividade aqui.

EXEMPLO 4: Atividades 4.56 e 4.57, p. 190-191.
Na atividade 4.32, o recurso digital acrescenta um ingrediente de dinâmica, que não poderia ser alcançado em uma abordagem apenas com lápis e papel. Entretanto, os gráficos das funções ainda são obtidos a partir de suas expressões analíticas – como na abordagem usual. As ferramentas do GeoGebra permitem ir ainda mais além: é possível traçar o gráfico de uma função sem que antes seja necessário determinar sua fórmula. Neste caso, os gráficos são obtidos comolugares geométricos, a partir da variação de um objeto dependente em uma construção geométrica.
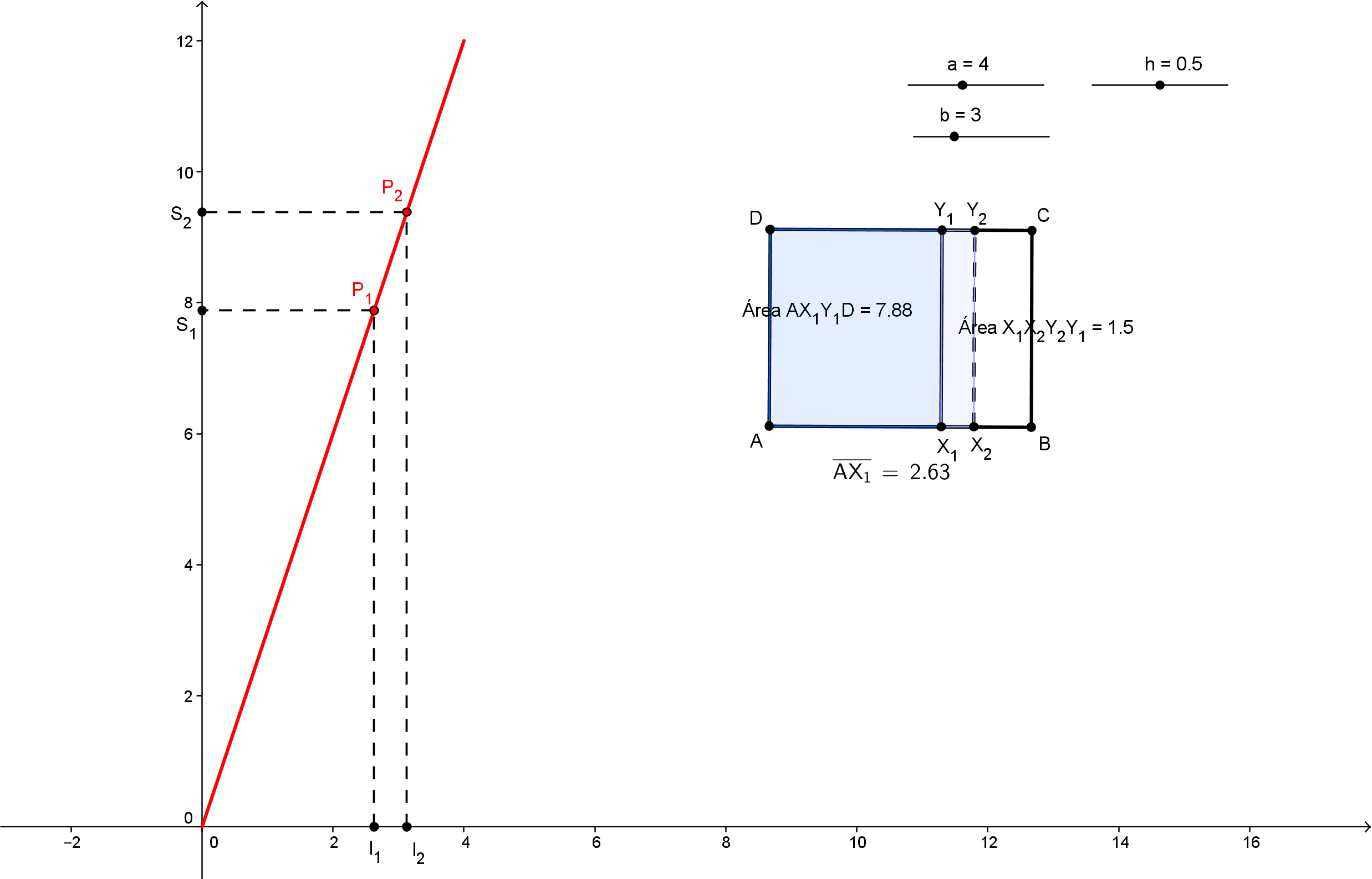
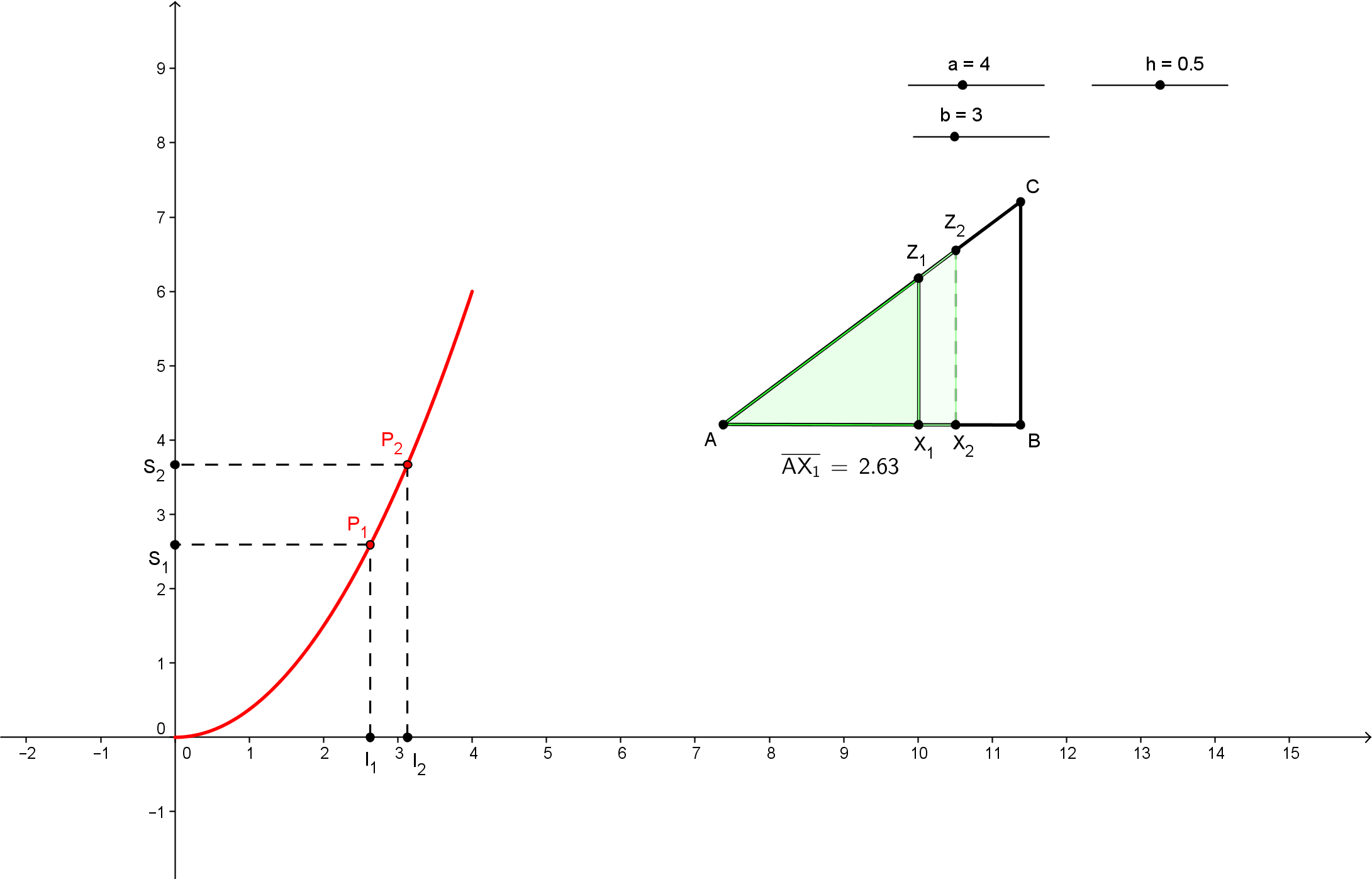
O objetivo das atividades 4.56 e 4.57 é estudar o comportamento de funções com base na análise qualitativa de sua variação média. As funções tratadas representam áreas variáveis de figuras planas em construções geométricas. Embora a noção de variação seja fundamental para o conceito de função, tem recebido pouca ênfase na escola básica. A análise da variação permite caracterizar as principais classes de funções elementares tratadas no ensino médio – possibilitando aos alunos uma experiência mais concreta com o comportamento dessas funções do que a simples apresentação das expressões analíticas e esboço dos gráficos por meio de substituição de valores. Os ambientes de geometria dinâmica podem enriquecer a abordagem de funções reais por meio da noção de variação, articulando diretamente relações de dependência funcional estabelecidas em construções geométricas e os respectivos gráficos, definidos como lugares geométricos, sem a medição de fórmulas (que podem ser determinadas como último passo das atividades).
Nestas atividades, são propostas duas situações:
- Na primeira, acréscimos iguais na variável independente correspondem a acréscimos iguais na variável dependente. Portanto, a variação é média é constante, e o gráfico da função é uma reta.
- Na segunda, para cada acréscimo fixado na variável independente, o acrescimento na variável dependente cresce quando o valor da variável independente cresce. Portanto, a variação média é crescente em relação à variável dependente, e o gráfico possui concavidade voltara para cima.
Veja os textos das atividades aqui.
Veja os arquivos das atividades aqui, aqui, aqui e aqui.
EXEMPLO 5: Atividade 5.6, p. 220-221.
Os chamados sistemas de computação algébrica são uma classe de softwares que integram ferramentas numéricas e simbólicas. As ferramentas numéricas operam com os objetos matemáticos fazendo aproximações decimais para os números envolvidos (como poderosas calculadoras), enquanto as ferramentas simbólicas manipulam as próprias representações analíticas desses objetos. Em geral, os sistemas de computação algébrica incluem ferramentas matemáticas sofisticadas e seu uso exige o conhecimento de sintaxes de programação específicas. No entanto, algumas dos recursos disponíveis nesses softwares podem ser usados em atividades acessíveis e interessantes para o ensino médio.
Por exemplo, é possível propor abordagens alternativas para a resolução de equações reais, integrando representações gráficas com a busca (criteriosa) por aproximações decimais para as raízes. No ensino médio, em geral, o repertório de equações a que os alunos são apresentados é bastante restrito: se reduz a equações polinomiais de graus 1 ou 2 e alguns casos particulares de equações exponenciais, logarítmicas e trigonométricas, resolvidas por meio de procedimentos específicos memorizados. O uso de sistemas de computação algébrica viabiliza a expansão desse repertório, incluindo equações cujas soluções não podem ser obtidas por métodos analíticos, mas que podem ser aproximadas por métodos numéricos.
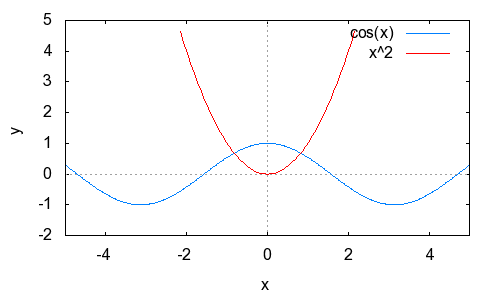
Esta atividade propõe a busca por aproximações numéricas para as soluções de uma equação, destacando o fato de que essa procura não pode se reduzir a um mero processo de “tentativa e erro”, e deve levar em conta a análise das propriedades da equação (feita, neste caso, por meio da visualização dos gráficos). Atividades como essa pode contribuir para expandir a própria compreensão dos alunos sobre os conceitos de equação e de raiz.
Veja o texto da atividade aqui.
Veja o arquivo da atividade aqui.